练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    一组数据2，3，x，5，7的平均数是4，则这组数据的众数是             .


       3         

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    对于平面直角坐标系中任意两点P1（x1，y1）、P2（x2，y2），称|x1﹣x2|+|y1﹣y2|为P1、P2两点的直角距离，记作：d（P1，P2）．若P0（x0，y0）是一定点，Q（x，y）是直线y=kx+b上的一动点，称d（P0，Q）的最小值为P0到直线y=kx+b的直角距离．令P0（2，﹣3）．O为坐标原点．则：

    （1）d（O，P0）=　　；

    （2）若P（a，﹣3）到直线y=x+1的直角距离为6，则a=　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在5×4的方格纸中，每个小正方形边长为1，点O，A，B在方格纸的交点（格点）上，在第四象限内的格点上找点C，使△ABC的面积为3，则这样的点C共有（　　）

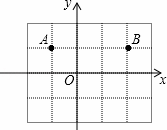
    　   A．                       2个                             B．                             3个  C． 4个 D． 5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    杨梅是漳州的特色时令水果，杨梅一上市，水果店的老板用1200元购进一批杨梅，很快售完；老板又用2500元购进第二批杨梅，所购件数是第一批的2倍，但进价比第一批每件多了5元．

    （1）第一批杨梅每件进价多少元？

    （2）老板以每件150元的价格销售第二批杨梅，售出80%后，为了尽快售完，决定打折促销，要使第二批杨梅的销售利润不少于320元，剩余的杨梅每件售价至少打几折？（利润=售价﹣进价）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，AB＝AC，∠A＝40°，AB的垂直

    平分线交AB于点D，交AC于点E，连接BE，则∠CBE

    的度数为

    A. 70°                                             B. 80°           C. 40°         D. 30°

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


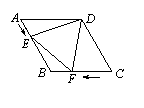
    如图，在菱形ABCD中，AB=4cm，∠ADC=120°，点E、F

    同时由A、C两点出发，分别沿AB、CB方向向点B匀速移动

    （到点B为止），点E的速度为1cm/s，点F的速度为2cm/s，

    经过t秒△DEF为等边三角形，则t 的值为             .

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，∠ABC=90°,以AB为直径的⊙O

    与AC边交于点D，过点D的直线交BC边于点E，

    ∠BDE=∠A．

    （1）判断直线DE与⊙O的位置关系，并说明理由.

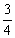    （2）若⊙O的半径R=5，tan A=   ，求线段CD的长.

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，的半径为1，是的内接等边三角形，

    点D，E在圆上，四边形为矩形，这个矩形的面积是

     A．2   　　 B．     C．  　　　 D．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


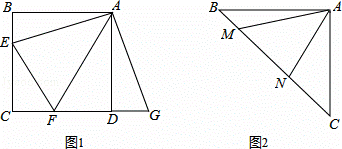
    （1）如图，正方形ABCD中，点E，F分别在边BC，CD上，∠EAF=45°，延长CD到点G，使DG=BE，连结EF，AG．求证：EF=FG．

    （2）如图，等腰直角三角形ABC中，∠BAC=90°，AB=AC，点M，N在边BC上，且∠MAN=45°，若BM=1，CN=3，求MN的长．

    查看答案和解析>>

    同步练习册答案