
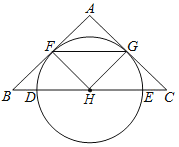
【题目】如图,在△ABC中,AB=AC,BC是经过⊙H的圆心,交⊙H于点D、E,AB、AC是圆的切线,F、G是切点.
(1)求证:BH=CH;
(2)填空:①当∠FHG= 时,四边形FHCG是平行四边形;
②当∠FED= 时,四边形AFHG是正方形.
【答案】(1)见解析;(2)①90°;②22.5°
【解析】
(1)证明△BFH≌△CGH可得结论.
(2)①当∠FHG=90°时,四边形FHCG是平行四边形.分别证明FG∥CH,FH∥CG即可.
②当∠FED=22.5°时,四边形AFHG是正方形.连接EF,首先证明∠AFH=∠FHG=∠AGH=90°,推出四边形AFHG是矩形,再根据HF=HG推出四边形AFHG是正方形.
(1)证明:∵AB=AC,
∴∠B=∠C.
∵AB、AC是⊙H的切线,
∴∠BFH=∠CGH=90°.
∵HF=HG,
∴△BFH≌△CGH(AAS),
∴BH=CH.
(2)解:①当∠FHG=90°时,四边形FHCG是平行四边形.
理由:∵△BFH≌△CGH(已证),
∴BF=CG,
∵AB=AC,
∴AF=AG,
∴∠AFG=∠AGF,
∵∠B=∠C,∠A+2∠AGF=180°,∠A+2∠C=180°,
∴∠AGF=∠C,
∴![]() ,
,
∵AC是⊙H的切线,
∴AC⊥HG,
∴∠FHG=∠CGH=90°,
∴![]() ,
,
∴四边形FHCG是平行四边形.
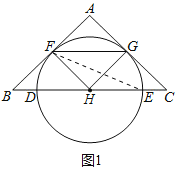
②当∠FE D=22.5°时,四边形AFHG是正方形.
理由:如图1中,连接EF.
![]() ,
,
![]() ,
,
∴∠FHD=2∠FED=45°,
∵△BFH≌△CGH(已证),
∴∠FHB=∠GHC=45°,
∴∠FHG=90°,
∵AB,AC是⊙H的切线,
∴AB⊥HF,AC⊥HG,
∴∠AFH=∠AGH=90°,
∴四边形AFHG是矩形,
∵HF=HG,
∴四边形AFHG是正方形.


科目:初中数学 来源: 题型:
【题目】已知∠AOB=90°,OM是∠AOB的平分线,将一个直角三角板的直角顶点P放在射线OM上,OP=2,移动直角三角板,两边分别交射线OA,OB与点C,D.
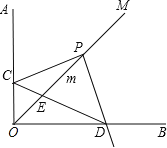
(1)如图,当点C、D都不与点O重合时,求证:PC=PD;
(2)联结CD,交OM于E,设CD=x,PE=y,求y与x之间的函数关系式;
(3)如图,若三角板的一条直角边与射线OB交于点D,另一直角边与直线OA,直线OB分别交于点C,F,且△PDF与△OCD相似,求OD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
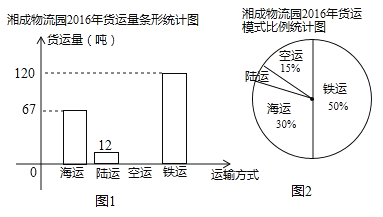
【题目】在“一带一路”倡议下,我国已成为设施联通,贸易畅通的促进者,同时也带动了我国与沿线国家的货物交换的增速发展,如图是湘成物流园2016年通过“海、陆(汽车)、空、铁”四种模式运输货物的统计图.
请根据统计图解决下面的问题:
(1)该物流园2016年货运总量是多少万吨?
(2)该物流园2016年空运货物的总量是多少万吨?并补全条形统计图;
(3)求条形统计图中陆运货物量对应的扇形圆心角的度数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+2(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,抛物线经过点D(﹣2,﹣3)和点E(3,2),点P是第一象限抛物线上的一个动点.
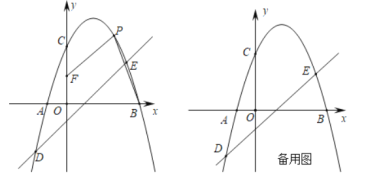
(1)求直线DE和抛物线的表达式;
(2)在y轴上取点F(0,1),连接PF,PB,当四边形OBPF的面积是7时,求点P的坐标;
(3)在(2)的条件下,当点P在抛物线对称轴的右侧时,直线DE上存在两点M,N(点M在点N的上方),且MN=2![]() ,动点Q从点P出发,沿P→M→N→A的路线运动到终点A,当点Q的运动路程最短时,请直接写出此时点N的坐标.
,动点Q从点P出发,沿P→M→N→A的路线运动到终点A,当点Q的运动路程最短时,请直接写出此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
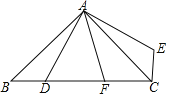
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.
(1)求证:△ABD≌△ACE;
(2)若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;
(3)在(2)的条件下,若BD=3,CF=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(﹣1,0)、C(0,3)、B(2,3)
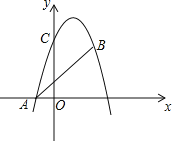
(1)求抛物线的解析式;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM为直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由(4个坐标).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,某商场计划购进甲、乙两种商品,已知购进甲商品1件和乙商品3件共需240元;购进甲商品2件和乙商品1件共需130元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
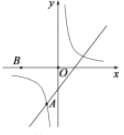
【题目】如图,反比例函数![]() 与一次函数
与一次函数![]() 在第三象限交于点
在第三象限交于点![]() .点
.点![]() 的坐标为(一3,0),点
的坐标为(一3,0),点![]() 是
是![]() 轴左侧的一点.若以
轴左侧的一点.若以![]() 为顶点的四边形为平行四边形.则点
为顶点的四边形为平行四边形.则点![]() 的坐标为_____________.
的坐标为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
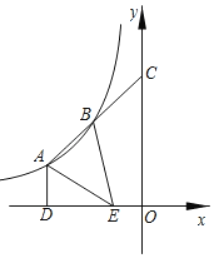
【题目】如图,点A、B是反比例函数y=![]() (k≠0)图象上的两点,延长线段AB交y轴于点C,且点B为线段AC中点,过点A作AD⊥x轴于点D,点E为线段OD的三等分点,且OE<DE.连接AE、BE,若S△ABE=7,则k的值为( )
(k≠0)图象上的两点,延长线段AB交y轴于点C,且点B为线段AC中点,过点A作AD⊥x轴于点D,点E为线段OD的三等分点,且OE<DE.连接AE、BE,若S△ABE=7,则k的值为( )
A.﹣12B.﹣10C.﹣9D.﹣6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com