
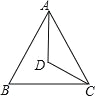
【题目】如图,△ABC 中,AB=AC,∠BAC 和∠ACB 的平分线相交于点D,∠ADC=125°,那么∠CAB 的大小是_________度.
【答案】40
【解析】
根据三角形的内角和定理求得∠ACD+∠CAD=55°,再由角平分线的定义求得∠BAC+∠ACB=2(∠CAD+∠ACD)=110°,即可求出∠ABC,最后用等腰三角形的性质即可得出结论.
在△ACD 中,∠ADC=125°,
∴∠ACD+∠CAD=180°﹣125°=55°
∴∠BAC 和∠ACB 的平分线相交于点 D,
∴∠BAC=2∠CAD,∠ACB=2∠ACD,
∴∠BAC+∠ACB=2(∠CAD+∠ACD)=2×55°=110°,
∴∠ABC=180°﹣(∠BAC+∠ACB)=70°,
∵AB=AC,
∴∠ABC=∠ACB=70°,
∴∠CAB=180°﹣∠ABC﹣∠ACB=40°,
故答案为 40.


科目:初中数学 来源: 题型:
【题目】已知如图1菱形ABCD,∠ABC=60°,边长为 3,在菱形内作等边三角形△AEF,边长为2 ![]() ,点E,点F,分别在AB,AC上,以A为旋转中心将△AEF顺时针转动,旋转角为α,如图2
,点E,点F,分别在AB,AC上,以A为旋转中心将△AEF顺时针转动,旋转角为α,如图2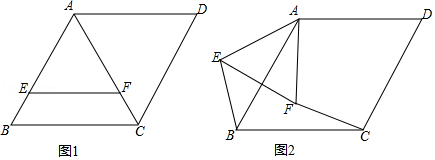
(1)在图2中证明BE=CF;
(2)若∠BAE=45°,求CF的长度;
(3)当CF= ![]() 时,直接写出旋转角α的度数.
时,直接写出旋转角α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,正方形OABC的面积为16,点D的坐标为(0,3).将直线BD沿y轴向下平移d个单位得到直线l(0<d≤4).
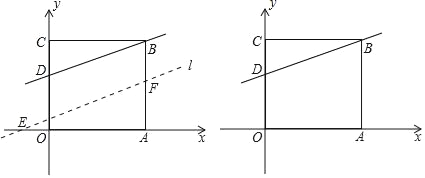
(1)则点B的坐标为 ;
(2)当d=1时,求直线l的函数表达式;
(3)设直线l与x轴相交于点E,与边AB相交于点F,若CE=CF,求d的值并直接写出此时∠ECF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥CD,∠BED=90°.填空:
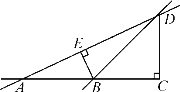
(1)∠ACD=_____度;
(2)直线AD与BE的位置关系是__________;
(3)点B到直线AD的距离是线段________的长度,点D到直线AB的距离是线段______的长度;
(4)在线段DA,DB,DC中,最短的是线段______;在线段BA,BE,BD中,最短的是线段______,理由是_____________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F. 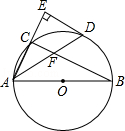
(1)猜想ED与⊙O的位置关系,并证明你的猜想;
(2)若AB=6,AD=5,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以A为圆心,AB为半径画弧,交AD于F,再分别以B、F为圆心,大于 ![]() BF的长为半径画弧,两弧相交于点G,若BF=6,AB=5,则AE的长为( )
BF的长为半径画弧,两弧相交于点G,若BF=6,AB=5,则AE的长为( ) 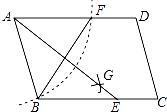
A.11
B.6
C.8
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校“数学魔盗团”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买1个A种魔方比1个B种魔方多花5元.

(1)求这两种魔方的单价;
(2)结合社员们的需求,社团决定购买A,B两种魔方共100个(其中A种魔方不超过50个).“双11期间”某商店有两种优惠活动,如图所示.请根据以上信息填空:购买A种魔方________个时选择活动一盒活动二购买所需费用相同.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com