练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某商店经营一种成本为每千克40美元的水产品，根据市场分析，若按每千克50元销售，一个月能售出500千克；销售价每涨1元，月销售量就减少10千克，针对这种水产品的销售情况，销售单价定为多少元时，获得的利润最大？最大利润是多少？

    【答案】解：设销售单价定为每千克x元，获得利润为w元，则：

    ∴当x=70时，利润最大为9000元．
    答：销售单价定为70元时获得的利润最大，最大利润是9000元
    【解析】解决最值问题的基本策略是函数思想，构建以销售单价x为自变量，利润为因变量的函数，再利用配方法求出最值.
    【考点精析】通过灵活运用二次函数的最值，掌握如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为弘扬中华民族传统文化，某校举办了“古诗文大赛”，并为获奖同学购买签字笔和笔记本作为奖品．1支签字笔和2个笔记本共8.5元，2支签字笔和3个笔记本共13.5元．

    （1）求签字笔和笔记本的单价分别是多少元？

    （2）为了激发学生的学习热情，学校决定给每名获奖同学再购买一本文学类且定价为15元的图书．书店出台如下促销方案：购买图书总数超过50本可以享受8折优惠，学校如果多买12本，则可以享受优惠且所花钱数与原来相同，问学校获奖的同学有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】AD与BE是△ABC的角平分线，D，E分别在BC，AC上，若AD=AB，BE=BC，则∠C=（　　）

    A. 69° B. C. D. 不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知如图一，在△ABC中，AD是角平分线，AE是高，∠ABC＝30°，∠ACB＝70°．

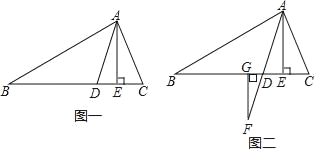
    (1)求∠DAE的度数．

    (2)如图二，若点F为AD延长线上一点，过点F作FG⊥BC于点G，求∠AFG的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】完成下面的证明过程．

    如图，已知，∠1+∠2＝180°，∠A＝∠D．求证AB∥CD．

    证明：∵∠1+∠2＝180°（已知）

    ∠1＝∠3（　 　）

    ∴∠3+∠2＝180°（　 　）

    ∴AE∥　 　（　 　）

    ∴∠D＝　 　（　 　）

    ∵∠A＝∠D（已知）

    ∴∠A＝∠CEA（　 　）

    ∴AB∥CD （　 　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头方向，每次移动1个单位长度，依次得到点A1(0，1)，A2(1，1)，A3(1，0)，A4(2，0)，A5(2，1)，…，则点A2018的坐标是_____．

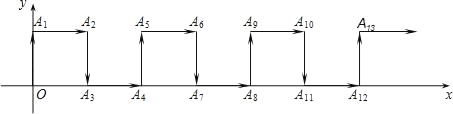
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】第二届全国青年运动会（简称：二青会）将于2019年8月在山西太原开幕，甲、乙两名自行车运动员正在积极备战．如图是教练员记录的甲、乙两选手在骑车时，在某时段速度随时间变化的图象，下列结论错误的是（ ）

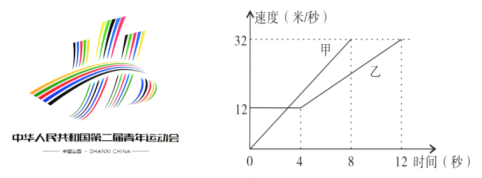
    A.乙前秒行驶的路程为米

    B.在到秒内甲的速度每秒增加米/秒

    C.甲、乙到第秒时行驶的路程相等

    D.在至秒内甲的速度都大于乙的速度

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直角坐标系中，△ABC的顶点都在网格点上，其中，C点坐标为（1，2）

    （1）写出点A、B的坐标：A（　　　，　　）、B（　　　，　　　）

    （2）将△ABC先向左平移1个单位长度，再向上平移2个单位长度，得到△A′B′C′，画出△A′B′C′

    （3）写出三个顶点坐标A′（　　　、　　　）、B′（　　　　、　　　）、C′ (　　　　、　　　）

    （4）求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图示，正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上，EF与BC相交于点G，连接CF．
    ①求证：△DAE≌△DCF；
    ②求证：△ABG∽△CFG．

    查看答案和解析>>

    同步练习册答案