
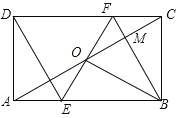
【题目】矩形 ABCD中,O为 AC 的中点,过点O的直线分别与AB,CD交于点E,F,连接 BF交AC于点M连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①△AOE≌△COF;②△EOB≌△CMB;③FB⊥OC,OM=CM;④四边形 EBFD 是菱形;⑤MB:OE=3:2其中正确结论的个数是( )
A. 5 B. 4 C. 3 D. 2
【答案】B
【解析】
作辅助线找全等三角形和特殊的直角三角形解题,见详解.
解:连接BD

∵四边形ABCD是矩形
∴AC=BD,AC、BD互相平分
∵O为AC中点
∴BD也过O点
∴OB=OC
∵∠COB=60°,OB=OC
∴△OBC是等边三角形
∴OB=BC=OC,∠OBC=60°
∵FO=FC,BF=BF
∴△OBF≌△CBF(SSS)
∴△OBF与△CBF关于直线BF对称
∴FB⊥OC,OM=CM.故③正确
∵∠OBC=60°
∴∠ABO=30°
∵△OBF≌△CBF
∴∠OBM=∠CBM=30°
∴∠ABO=∠OBF
∵AB∥CD
∴∠OCF=∠OAE
∵OA=OC
可得△AOE≌△COF,故①正确
∴OE=OF
则四边形EBFD是平行四边形,又可知OB⊥EF
∴四边形EBFD是菱形.故④正确
∴△EOB≌△FOB≌△FCB.则②△EOB≌△CMB错误
∵∠OMB=∠BOF=90°,∠OBF=30°,
设MB=![]() a,则OM=a,OB=2a,
a,则OM=a,OB=2a,
OF=![]() OM,
OM,
∵OE=OF
∴MB:OE=3:2.则⑤正确
综上一共有4个正确的,
故选B.


科目:初中数学 来源: 题型:
【题目】从大拇指开始,按照大拇指→食指→中指→无名指→小指→无名指→中指→食指→大拇指→ 食指的顺序,依次数整数 1,2,3,4,5,6,7,,当数到 2019 时,对应的手指为________________; 当第 n 次数到食指时,数到的数是_________________________ (用含 n 的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位采购员同去一家饲料公司购买两次饲料.两次饲料的价格有变化,两位采购员的购货方式也不同,其中,甲每次购买1000千克,乙每次用去800元,而不管购买多少饲料.
(1)甲、乙所购饲料的平均单价各是多少?
(2)谁的购货方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
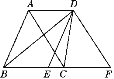
【题目】如图,在封闭图形ABCD中,AD∥BC,且AD=4,三角形ABC的周长为14,将三角形ABC平移到三角形DEF的位置.
(1)指出平移的方向和平移的距离;
(2)求封闭图形ABFD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点A从原点出发向数轴负方向运动,同时动点B也从原点出发向数轴正方向运动,2秒后,两点相距16个单位长度,已知动点A、B的速度比为1:3(速度单位:1个单位长度秒).
![]()
(1)求两个动点运动的速度;
(2)在数轴上标出A、B两点从原点出发运动2秒时的位置;
(3)若表示数0的点记为O,A、B两点分别从(2)中标出的位置同时向数轴负方向运动,再经过多长时间,满足OB=2OA?
查看答案和解析>>
科目:初中数学 来源: 题型:
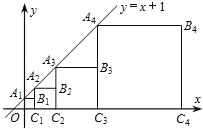
【题目】如图,直线 y=x+1 与 y 轴交于点 A1,以 OA1为边,在 y 轴右侧作正方形 OA1B1C1,延长 C1B1交直线 y=x+1 于点 A2,再以 C1A2为边作正方形,…,这些正方形与直线 y=x+1 的交点分别为 A1,A2,A3,…,An,则点 Bn 的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBEF是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
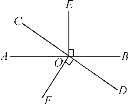
【题目】如图,直线AB,CD相交于点O,OE⊥AB,OF⊥CD.
(1)若OC恰好是∠AOE的平分线,则OA是∠COF的平分线吗?请说明理由;
(2)若∠EOF=5∠BOD,求∠COE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图![]() 示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.
示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.
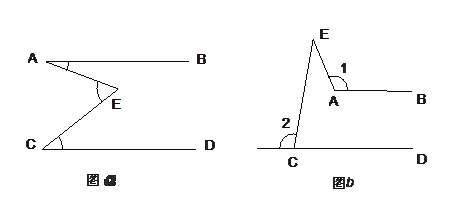
(2)现在如图b示,仍有AB∥CD,但点E在AB与CD的上方,①请尝试探索∠1,∠2,∠E三者的数量关系. ②请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com