
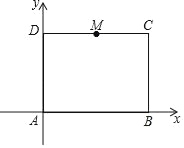
【题目】如图,在平面直角坐标系中有矩形ABCD,A(0,0),C(8,6),M为边CD上一动点,当△ABM是等腰三角形时,M点的坐标为_____.
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD的延长线交于点F,且∠AFB=∠ABC.
(1)求证:直线BF是⊙O的切线.
(2)若CD=2![]() ,OP=1,求线段BF的长.
,OP=1,求线段BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
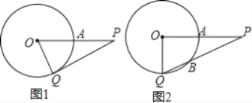
【题目】已知P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.
(1)如图1,若PQ是⊙O的切线,求∠QOP的大小;
(2)如图2,若∠QOP=90°,求PQ被⊙O截得的弦QB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
问题情境:
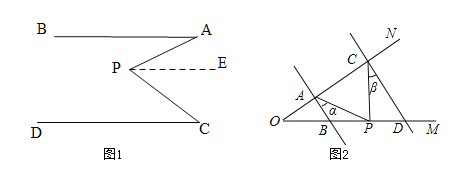
如图 1,AB∥CD,∠PAB=25°,∠PCD=37°,求∠APC的度数,小明的思路是:过点P作PE∥AB,通过平行线性质来求∠APC
问题解决:
(1)按小明的思路,易求得∠APC 的度数为 °;
问题迁移:
如图 2,AB∥CD,点 P 在射线 OM 上运动,记∠PAB=α,∠PCD=β.
(2)当点 P 在 B,D 两点之间运动时,问∠APC 与α,β 之间有何数量关系? 请说明理由;
拓展延伸:
(3)在(2)的条件下,如果点 P 在 B,D 两点外侧运动时 (点 P 与点 O,B,D 三点不重合)请你直接写出当点 P 在线段 OB 上时,∠APC 与 α,β 之间的数量关系 ,点 P 在射线 DM 上时,∠APC 与 α,β 之间的数量关系 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的各边,在边BC的同侧分别作三个正方形ABDI,BCFE,ACHG.

(1)求证:△BDE≌△BAC;
(2)求证:四边形ADEG是平行四边形.
(3)直接回答下面两个问题,不必证明:
①当△ABC满足条件_____________________时,四边形ADEG是矩形.
②当△ABC满足条件_____________________时,四边形ADEG是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
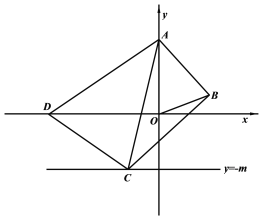
【题目】已知:如图,在平面直角坐标系中,O为坐标原点,△OAB的顶点A、B的坐标分别是A(0,5),B(3,1),过点B画BC⊥AB交直线![]() 于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.
于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.
(1)求证:△ABC≌△AOD.
(2)设△ACD的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(3)若四边形ABCD恰有一组对边平行,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
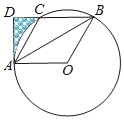
【题目】如图,⊙O的半径为6,点A,B,C为⊙O上三点,BA平分∠OBC,过点A作AD⊥BC交BC延长线于点D.
(1)求证:AD是⊙O的切线;
(2)当sin∠OBC=![]() 时,求BC的长;
时,求BC的长;
(3)连结AC,当AC∥OB时,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com