
 飞行员在空中观察地面的区域是一个圆(如图),当观察角α为50°,飞机的飞行高度h为9.8×102m时,观察区域的半径为多少米(结果精确到1m)?如果观察角度不变,要使观察区域面积增加1倍,那么飞机要升高多少米(精确到1m)?
飞行员在空中观察地面的区域是一个圆(如图),当观察角α为50°,飞机的飞行高度h为9.8×102m时,观察区域的半径为多少米(结果精确到1m)?如果观察角度不变,要使观察区域面积增加1倍,那么飞机要升高多少米(精确到1m)? 分析 求出∠ACO度数,由三角函数求出半径OA,那么面积=π×底面半径2,把相关数值代入计算即可;区域面积增加1倍,那么半径是原来的 $\sqrt{2}$倍,求出飞机飞行高度,减去原来的高度即为升高的高度.
解答 解: 如图所示:连接OC,则OC⊥AB,
如图所示:连接OC,则OC⊥AB,
∵飞机的高度h=9.8×102m,观测角α=50°,
∵∠ACO=$\frac{1}{2}$α=25°,tan∠ACO=$\frac{OA}{OC}$,
∴OA=OC′tan25°=9.8×102×0.4663≈457(米),
∴看到的区域面积是π×OA2平方米,
∵区域面积增加1倍,
∴半径是原来的 $\sqrt{2}$倍,
∴半径为457×$\sqrt{2}$≈646(米),
∴飞机飞行的高度=$\frac{646}{tan25°}$≈1385(米),
∴飞机需升高的高度为1385-980=405(米).
点评 本题考查了解直角三角形的应用、圆的面积;理解圆面积是原来的2倍,则半径是原来的 $\sqrt{2}$倍是解决本题的突破点.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
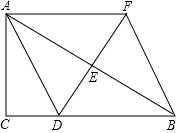 如图,在△ABC中,∠C=90°,点D为边BC上一点,点E为边AB的中点,过点A作AF∥BC,交DE的延长线于点F,联结BF.
如图,在△ABC中,∠C=90°,点D为边BC上一点,点E为边AB的中点,过点A作AF∥BC,交DE的延长线于点F,联结BF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
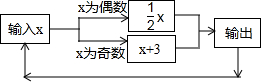 如图所示的运算程序中,若开始输入的x值为15,则第1次输出的结果为18,第2次输出的结果为9,…,第2017次输出的结果为( )
如图所示的运算程序中,若开始输入的x值为15,则第1次输出的结果为18,第2次输出的结果为9,…,第2017次输出的结果为( )| A. | 3 | B. | 4 | C. | 6 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
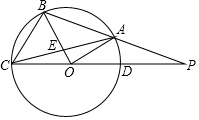 如图,A、B、C为⊙O上的点,PC过O点,交⊙O于D点,PD=OD,若OB⊥AC于E点.
如图,A、B、C为⊙O上的点,PC过O点,交⊙O于D点,PD=OD,若OB⊥AC于E点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com