
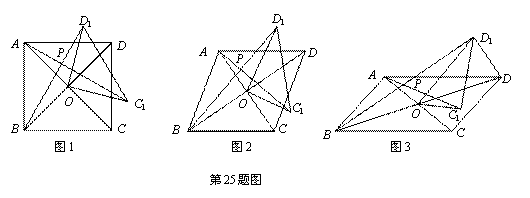
在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1,旋转角为θ(0°<θ<90°),连接AC1、BD1,AC1与BD1交于点P.
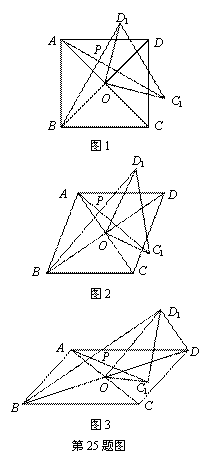
(1)如图1,若四边形ABCD是正方形.
①求证:△AOC1≌△BOD1.
②请直接写出AC1 与BD1的位置关系.
(2)如图2,若四边形ABCD是菱形,AC=5,BD=7,设AC1=k BD1.判断AC1与BD1的位置关系,说明理由,并求出k的值.
(3)如图3,若四边形ABCD是平行四边形,AC=5,BD=10,连接DD1,设AC1=kBD1.

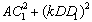 请直接写出k的值和 的值.
请直接写出k的值和 的值.
 |


解:
(1)①证明:
∵四边形ABCD是正方形
∴AC=BD,OC=OA=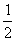 AC,OD=OB=
AC,OD=OB=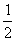 BD
BD
 ∴OC=OA=OD=OB,
∴OC=OA=OD=OB,
∵△C1OD1由△COD绕点O旋转得到
∴O C1= OC,O D1=OD,∠CO C1=∠DO D1
∴O C1= O D1 ∠AO C1=∠BO D1
∴△AO C1≌△BOD1
②AC1⊥BD1
(2)AC 1⊥BD1
1⊥BD1
理由如下:∵四边形ABCD是菱形
∴OC=OA=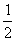 AC,OD=OB=
AC,OD=OB=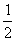 BD,AC⊥BD
BD,AC⊥BD
∵△C1OD1由△COD绕点O旋转得到
∴O C1= OC,O D1=OD,∠CO C1=∠DO D1
∴O C1=OA ,O D1=OB,∠AO C1=∠BO D1
∴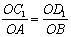
∴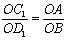
∴△AO C1∽△BOD1 ∴∠O AC1= ∠OB D1
又∵∠AOB=90°
∴∠O AB+∠ABP+∠OB D1=90°
∴∠O AB+∠ABP+∠O AC1=90°
∴∠APB=90°
AC1⊥BD1
∵△AO C1∽△BOD1
∴
∴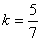
(3)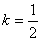
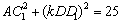




科目:初中数学 来源: 题型:
课本中有一道作业题:
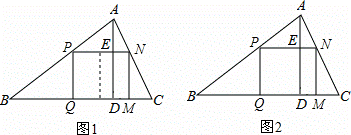
有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.
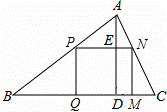
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.


查看答案和解析>>
科目:初中数学 来源: 题型:
某服装厂接到一份加工3000件服装的订单.应客户要求,需提前供货,该服装厂决定提高加工速度,实际每天加工的件数是原计划的1.5倍,结果提前10天完工.原计划每天加工多少件服装?


查看答案和解析>>
科目:初中数学 来源: 题型:
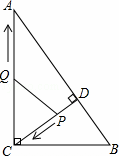
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ:S△ABC=9:100?若存在,求出t的值;若不存在,说明理由.
(3)当t为何值时,△CPQ为等腰三角形?


查看答案和解析>>
科目:初中数学 来源: 题型:
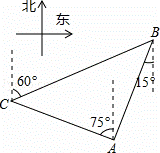
如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为( )
|
| A. | 20海里 | B. | 10 | C. | 20 | D. | 30海里 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com