
【题目】如图,已知A(-4,![]() ),B(-1,2)是一次函数y=kx+b与反比例函数y=
),B(-1,2)是一次函数y=kx+b与反比例函数y=![]() (m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D。
(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D。

(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标。
【答案】(1)、-4<x<-1;(2)、y=![]() ;m=-2;(3)、(
;m=-2;(3)、(![]() ,
,![]() ).
).
【解析】
试题分析:(1)、根据图示直接得出答案;(2)、将A、B两点坐标代入一次函数解析式求出k和b的值,将点B的坐标代入反比例函数解析式求出m的值;(3)、首先根据一次函数设出点P的坐标,求出AC、OC、BD、OD的长度,根据△PCA和△PDB的面积相等列出关于x的方程求出x的值,然后得出点P的坐标.
试题解析:(1)、由图象,当-4<x<-1时,一次函数值大于反比例函数的值
(2)、把A(-4,![]() ),B(-1,2)代入y=kx+b得,
),B(-1,2)代入y=kx+b得, 解得:
解得:![]()
∴ 一次函数的解析式为y=![]()
把B(-1,2)代入y=![]() 得m=-2,即m的值为-2
得m=-2,即m的值为-2
(3)、设P的坐标为(x,![]() ),由A、B的坐标可知AC=
),由A、B的坐标可知AC=![]() ,OC=4,BD=1,OD=2,
,OC=4,BD=1,OD=2,
易知△PCA的高为x+4,△PDB的高2-(![]() ),由
),由![]() 可得
可得
![]() ,解得
,解得![]() ,此时
,此时![]()
∴ P点坐标为(![]() ,
,![]() )
)


科目:初中数学 来源: 题型:
【题目】下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且平分的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
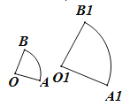
【题目】若两个扇形满足弧长的比等于它们半径的比,则这称这两个扇形相似。如图,如果扇形AOB与扇形![]() 是相似扇形,且半径
是相似扇形,且半径![]() (
(![]() 为不等于0的常数)那么下面四个结论:①∠AOB=∠
为不等于0的常数)那么下面四个结论:①∠AOB=∠![]() ;②△AOB∽△
;②△AOB∽△![]() ;③
;③![]() ;④扇形AOB与扇形
;④扇形AOB与扇形![]() 的面积之比为
的面积之比为![]() 。成立的个数为:( )
。成立的个数为:( )
A、1个 B、2个 C、3个 D、4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1、l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是( )
A.2 B.3 C.4 D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com