
ЁОЬтФПЁПдФЖСЯТУцВФСЯЃК
ЙлВьгыЫМПМЃКдФЖСЯТСаВФСЯЃЌВЂНтОіКѓУцЕФЮЪЬт.дкШёНЧ![]() жаЃЌ
жаЃЌ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФЖдБпЗжБ№ЪЧaЁЂbЁЂcЃЌЙ§Aзї
ЕФЖдБпЗжБ№ЪЧaЁЂbЁЂcЃЌЙ§Aзї![]() гкDЃЈШчЭМЃЉЃЌдђ
гкDЃЈШчЭМЃЉЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ![]() ЃЌгкЪЧ
ЃЌгкЪЧ![]() ЃЌМД
ЃЌМД![]() .ЭЌРэгаЃК
.ЭЌРэгаЃК![]() ЃЌ
ЃЌ![]() ЃЌЫљвд
ЃЌЫљвд![]() .
.
МДЃКдквЛИіШ§НЧаЮжаЃЌИїБпКЭЫќЫљЖдНЧЕФе§ЯвЕФБШЯрЕШ.дкШёНЧШ§НЧаЮжаЃЌШєвбжЊШ§ИідЊЫиЃЈжСЩйгавЛЬѕБпЃЉЃЌдЫгУЩЯЪіНсТлКЭгаЙиЖЈРэОЭПЩвдЧѓГіЦфгрШ§ИіЮДжЊдЊЫи.ИљОнЩЯЪіВФСЯЃЌЭъГЩЯТСаИїЬт.
ЃЈ1ЃЉШчЭМЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЛ
ЃЛ
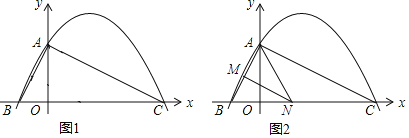
ЃЈ2ЃЉШчЭМЃЌвЛЛѕТждкCДІВтЕУЕЦЫўAдкЛѕТжЕФББЦЋЮї30ЁуЕФЗНЯђЩЯЃЌЫцКѓЛѕТжвд60КЃРя/ЪБЕФЫйЖШАДББЦЋЖЋ30ЁуЕФЗНЯђКНааЃЌАыаЁЪБКѓЕНДяBДІЃЌДЫЪБгжВтЕУЕЦЫўAдкЛѕТжЕФББЦЋЮї75ЁуЕФЗНЯђЩЯЃЈШчЭМЃЉЃЌЧѓДЫЪБЛѕТжОрЕЦЫўAЕФОрРыAB.
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЪдЧѓ75ЁуЕФе§ЯвжЕ.ЃЈНсЙћБЃСєИљКХЃЉ

ЁОД№АИЁПЃЈ1ЃЉ20![]() ЃЛЃЈ2ЃЉ15
ЃЛЃЈ2ЃЉ15![]() КЃРяЃЛЃЈ3ЃЉ
КЃРяЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнВФСЯЃКдквЛИіШ§НЧаЮжаЃЌИїБпКЭЫќЫљЖдНЧЕФе§ЯвЕФБШЯрЕШЃЌаДГіБШР§ЙиЯЕЃЌДњШыЪ§жЕМДПЩЧѓЕУABЕФжЕ.
ЃЈ2ЃЉДЫЬтПЩЯШгЩЫйЖШКЭЪБМфЧѓГіBCЕФОрРыЃЌдйгЩИїЗНЯђНЧЕУГіЁЯAЕФНЧЖШЃЌЙ§BзїBMЁЭACгкMЃЌЧѓГіЁЯMBC=30ЁуЃЌЧѓГіMCЃЌгЩЙДЙЩЖЈРэЧѓГіBMЃЌЧѓГіAMЁЂBMЕФГЄЃЌгЩЙДЙЩЖЈРэЧѓГіABМДПЩЃЛ
ЃЈ3ЃЉдкШ§НЧаЮABCжаЃЌЁЯA=45ЃЌЁЯABC=75ЃЌЁЯACB=60ЃЌЙ§ЕуCзїACЕФДЙЯпBDЃЌЙЙдьжБНЧШ§НЧаЮABDЃЌBCDЃЌдкжБНЧШ§НЧаЮABDжаПЩЧѓГіADЕФГЄЃЌНјЖјПЩЧѓГіsin75ЁуЕФжЕЃЎ
НтЃКЃЈ1ЃЉдкЁїABCжаЃЌЁЯB=75ЁуЃЌЁЯC=45ЁуЃЌBC=60ЃЌдђЁЯA=60ЁуЃЌ
Ёп![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() =
=![]() ЃЌ
ЃЌ
МД![]() =
=![]() ЃЌ
ЃЌ
НтЕУЃКAB=20![]() .
.
ЃЈ2ЃЉШчЭМЃЌ

вРЬтвтЃКBC=60ЁС0.5=30ЃЈКЃРяЃЉ
ЁпCDЁЮBEЃЌ
ЁрЁЯDCB+ЁЯCBE=180Ёу
ЁпЁЯDCB=30ЁуЃЌ
ЁрЁЯCBE=150Ёу
ЁпЁЯABE=75ЁуЃЎ
ЁрЁЯABC=75ЁуЃЌ
ЁрЁЯA=45ЁуЃЌ
дкЁїABCжаЃЌ![]() =
=![]() МД
МД![]() =
=![]() ЃЌ
ЃЌ
НтжЎЕУЃКAB=15![]() ЃЎ
ЃЎ
Д№ЃКЛѕТжОрЕЦЫўЕФОрРыAB=15![]() КЃРяЃЎ
КЃРяЃЎ
ЃЈ3ЃЉЙ§ЕуBзїACЕФДЙЯпBMЃЌДЙзуЮЊM.
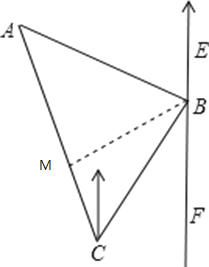
дкжБНЧШ§НЧаЮABMжаЃЌЁЯA=45ЁуЃЌAB=15![]() ЃЌ
ЃЌ
ЫљвдAM=15![]() ЃЌдкжБНЧШ§НЧаЮBDCжаЃЌЁЯBCM=60ЁуЃЌBC=30ЁуЃЌПЩЧѓЕУCM=15ЃЌ
ЃЌдкжБНЧШ§НЧаЮBDCжаЃЌЁЯBCM=60ЁуЃЌBC=30ЁуЃЌПЩЧѓЕУCM=15ЃЌ
ЫљвдAC=15![]() +15ЃЌ
+15ЃЌ
гЩЬтвтЕУЃЌ![]() ЃН
ЃН![]() ЃЌsin75Ёу=
ЃЌsin75Ёу=![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШЅФъЕФЬхг§жаПМжаЃЌФГаЃ6УћбЇЩњЕФЬхг§ГЩМЈЭГМЦШчЯТБэЃК
ГЩМЈ | 17 | 18 | 20 |
ШЫЪ§ | 2 | 3 | 1 |
дђЯТСаЙигкетзщЪ§ОнЕФЫЕЗЈДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ
A.жкЪ§ЪЧ18B.жаЮЛЪ§ЪЧ18C.ЦНОљЪ§ЪЧ18D.ЗНВюЪЧ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаСНИіКЏЪ§y1КЭy2ЃЌШєЖдгкУПИіЪЙКЏЪ§гавтвхЕФЪЕЪ§xЃЌКЏЪ§yЕФжЕЮЊСНИіКЏЪ§жЕжаНЯаЁЕФЪ§ЃЌдђГЦКЏЪ§yЮЊетСНИіКЏЪ§y1ЁЂy2ЕФНЯаЁжЕКЏЪ§ЃЎР§ШчЃКy1ЃНx+1ЃЌy2ЃНЉ2x+4ЃЌдђy1ЃЌy2ЕФНЯаЁжЕКЏЪ§ЮЊyЃН![]() ЃЎ
ЃЎ
ЃЈ1ЃЉКЏЪ§yЪЧКЏЪ§y1ЃН![]() ЃЌy2ЃНxЕФНЯаЁжЕКЏЪ§ЃЎ
ЃЌy2ЃНxЕФНЯаЁжЕКЏЪ§ЃЎ
ЂйдкШчЭМЕФЦНУцжБНЧзјБъЯЕжаЛГіКЏЪ§yЕФЭМЯѓЃЎ
ЂкаДГіКЏЪ§yЕФСНЬѕаджЪЃЎ
ЃЈ2ЃЉКЏЪ§yЪЧКЏЪ§y1ЃНx2Љ2x+1ЃЌy2ЃНx+1ЕФШЁНЯаЁжЕКЏЪ§ЃЎaЁмxЁм![]() ЪБЃЌКЏЪ§жЕyЕФШЁжЕЗЖЮЇЮЊ0ЁмyЁмbЃЎЕБaШЁФГИіЗЖЮЇФкЕФШЮвтжЕЪБЃЌbЮЊЖЈжЕЃЎжБНгаДГіТњзуЬѕМўЕФaЕФШЁжЕЗЖЮЇМАЦфЖдгІЕФbЕФжЕЃЎ
ЪБЃЌКЏЪ§жЕyЕФШЁжЕЗЖЮЇЮЊ0ЁмyЁмbЃЎЕБaШЁФГИіЗЖЮЇФкЕФШЮвтжЕЪБЃЌbЮЊЖЈжЕЃЎжБНгаДГіТњзуЬѕМўЕФaЕФШЁжЕЗЖЮЇМАЦфЖдгІЕФbЕФжЕЃЎ
ЃЈ3ЃЉКЏЪ§yЪЧКЏЪ§y1ЃНx2Љ2mxЃЌy2ЃНmxЃЈmЮЊГЃЪ§ЃЌЧвmЁй0ЃЉЕФНЯаЁжЕКЏЪ§ЃЎЕБ![]() mЉ2ЁмxЁм1ЪБЃЌЫцзХxЕФдіДѓЃЌКЏЪ§yЯШдіДѓКѓМѕаЁЃЌжБНгаДГіmЕФШЁжЕЗЖЮЇЃЎ
mЉ2ЁмxЁм1ЪБЃЌЫцзХxЕФдіДѓЃЌКЏЪ§yЯШдіДѓКѓМѕаЁЃЌжБНгаДГіmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
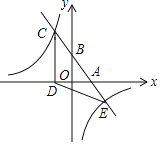
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=kx+bЃЈkЁЂbЮЊГЃЪ§ЃЌkЁй0ЃЉЕФЭМЯѓгыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌЧвгыЗДБШР§КЏЪ§y=![]() ЃЈnЮЊГЃЪ§ЃЌЧвnЁй0ЃЉЕФЭМЯѓдкЕкЖўЯѓЯоНЛгкЕуCЃЎCDЁЭxжсЃЌДЙзуЮЊDЃЌШєOB=2OA=3OD=12ЃЎ
ЃЈnЮЊГЃЪ§ЃЌЧвnЁй0ЃЉЕФЭМЯѓдкЕкЖўЯѓЯоНЛгкЕуCЃЎCDЁЭxжсЃЌДЙзуЮЊDЃЌШєOB=2OA=3OD=12ЃЎ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉМЧСНКЏЪ§ЭМЯѓЕФСэвЛИіНЛЕуЮЊEЃЌЧѓЁїCDEЕФУцЛ§ЃЛ
ЃЈ3ЃЉжБНгаДГіВЛЕШЪНkx+bЁм![]() ЕФНтМЏЃЎ
ЕФНтМЏЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПyЃНx2+ЃЈ1ЉaЃЉx+1ЪЧЙигкxЕФЖўДЮКЏЪ§ЃЌЕБxЕФШЁжЕЗЖЮЇЪЧ1ЁмxЁм3ЪБЃЌyдкxЃН1ЪБШЁЕУзюДѓжЕЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
A. aЁмЉ5B. aЁн5C. aЃН3D. aЁн3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊе§БШР§КЏЪ§yЃН![]() xЕФЭМЯѓгыЗДБШР§КЏЪ§yЃН
xЕФЭМЯѓгыЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓНЛгкAЃЈaЃЌЃ2ЃЉЃЌBСНЕуЃЎ
ЕФЭМЯѓНЛгкAЃЈaЃЌЃ2ЃЉЃЌBСНЕуЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФБэДяЪНКЭЕуBЕФзјБъЃЛ
ЃЈ2ЃЉPЪЧЕквЛЯѓЯоФкЗДБШР§КЏЪ§ЭМЯѓЩЯвЛЕуЃЌЙ§ЕуPзїyжсЕФЦНааЯпЃЌНЛжБЯпABгкЕуCЃЌСЌНгPOЃЌШєЁїPOCЕФУцЛ§ЮЊ3ЃЌЧѓЕуPЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
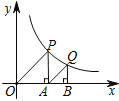
ЁОЬтФПЁПШчЭМЃЌЁїOAPгыЁїABQОљЮЊЕШбќжБНЧШ§НЧаЮЃЌЕуPЁЂQдкКЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЃЌжБНЧЖЅЕуAЁЂBОљдкxжсЩЯЃЌдђЕуBЕФзјБъЮЊ__________.
ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЃЌжБНЧЖЅЕуAЁЂBОљдкxжсЩЯЃЌдђЕуBЕФзјБъЮЊ__________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊЖўДЮКЏЪ§y=ax2+![]() x+cЃЈaЁй0ЃЉЕФЭМЯѓгыyжсНЛгкЕуAЃЈ0ЃЌ4ЃЉЃЌгыxжсНЛгкЕуBЁЂCЃЌЕуCзјБъЮЊЃЈ8ЃЌ0ЃЉЃЌСЌНгABЁЂACЃЎ
x+cЃЈaЁй0ЃЉЕФЭМЯѓгыyжсНЛгкЕуAЃЈ0ЃЌ4ЃЉЃЌгыxжсНЛгкЕуBЁЂCЃЌЕуCзјБъЮЊЃЈ8ЃЌ0ЃЉЃЌСЌНгABЁЂACЃЎ
ЃЈ1ЃЉЧыжБНгаДГіЖўДЮКЏЪ§y=ax2+![]() x+cЕФБэДяЪНЃЛ
x+cЕФБэДяЪНЃЛ
ЃЈ2ЃЉХаЖЯЁїABCЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЕуNдкxжсЩЯдЫЖЏЃЌЕБвдЕуAЁЂNЁЂCЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЪБЃЌЧыаДГіДЫЪБЕуNЕФзјБъЃЛ
ЃЈ4ЃЉШчЭМ2ЃЌШєЕуNдкЯпЖЮBCЩЯдЫЖЏЃЈВЛгыЕуBЁЂCжиКЯЃЉЃЌЙ§ЕуNзїNMЁЮACЃЌНЛABгкЕуMЃЌЕБЁїAMNУцЛ§зюДѓЪБЃЌЧѓДЫЪБЕуNЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНax2+bx+c(aЁй0)ЩЯВПЗжЕуЕФКсзјБъxгызнзјБъyЕФЖдгІжЕШчЯТБэЃК
x | Ё | Љ3 | Љ2 | Љ1 | 0 | 1 | 2 | 3 | Ё |
y | Ё |
| Љ4 |
| Љ4 |
| 0 |
| Ё |
(1)ЧѓИУХзЮяЯпЕФБэДяЪНЃЛ
(2)вбжЊЕуE(4ЃЌ y)ЪЧИУХзЮяЯпЩЯЕФЕуЃЌЕуEЙигкХзЮяЯпЕФЖдГЦжсЖдГЦЕФЕуЮЊЕуFЃЌЧѓЕуEКЭЕуFЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com