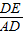已知等腰梯形的一个锐角等于60°，它的两底分别为15cm，49cm，则腰长= cm．
【答案】
分析：如图所示，等腰梯形ABCD，AB∥CD，AD=BC，AB=15cm，DC=49cm，∠D=60°求AD的长．
过A，B分别作高AE，BF，
因为AB∥CD得到AB=EF=15cm，根据全等三角形的判定得到△ADE≌△BCF，所以DE=FC，又因为DC=49cm，AB=15cm，得出DE=17cm．在Rt△ADE中，∠D=60°，DE=17cm，从而得出AD=34cm．
解答：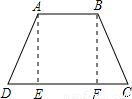
解：如图过A，B分别作AE⊥DC于E，BF⊥BC于F，
∵四边形ABCD是等腰梯形
∴AEFB为平行四边形
∴AB=EF
∴2DE=CD-AB=34，即DE=17
∴cos∠D=cos60°=
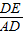
∴AD=34
即腰长为34cm．
点评：此题考查了学生对等腰梯形的性质及全等三角形的判定，三角函数等知识的掌握情况，做题时需对各个知识点进行灵活运用．
