
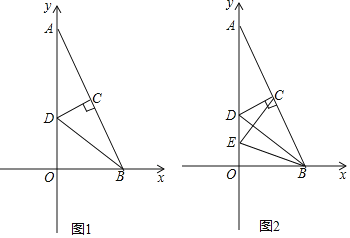
【题目】如图,在平面直角坐标系中,A(0,8),B(4,0),AB的垂直平分线交y轴与点D,连接BD,M(a,1)为第一象限内的点
(1)则D(____, ____),并求直线BD的解析式;
(2)当![]() 时,求a的值;
时,求a的值;
(3)点E为y轴上一个动点,当△CDE为等腰三角形时,求E点的坐标.
【答案】(0,3),BD的解析式为![]() ;(2)a=6;(3)E(0,
;(2)a=6;(3)E(0, ![]() )
)
【解析】试题分析:(1)设OD=x,则AD=8-x,由线段垂直平分线的性质得出BD=AD=8-x,在Rt△BOD中,由勾股定理得出方程,解方程即可;直线BD的解析式为y=kx+b,由待定系数法即可得出答案;
(2)由题意得出△DBC与△DBM是等高的三角形得出直线BD与直线CM平行,求出直线CM的解析式为y=-![]() x+
x+![]() ;把M(a,1)代入求出a=6即可;
;把M(a,1)代入求出a=6即可;
(3)由勾股定理求出AB,得出AC=2![]() ,由勾股定理求出CD=
,由勾股定理求出CD=![]() =
=![]() ,分三种情况:①DC=DE时;②CE=CD时;③EC=ED时;分别求出点E的坐标即可.
,分三种情况:①DC=DE时;②CE=CD时;③EC=ED时;分别求出点E的坐标即可.
试题解析:(1)∵A(0,8),B(4,0),
∴OA=8,OB=4,
设OD=x,则AD=8x,
∵AB的垂直平分线交y轴于点D,
∴BD=AD=8x,
在Rt△BOD中,由勾股定理得:x2+42=(8x)2,
解得:x=3,
∴D(0,3);
故答案为:0,3;
设BD的解析式为y=kx+b
把B(4,0)D(0,3)代入y=kx+b得:
![]()
解得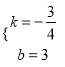
则y=![]() ,
,
(2) ∵S△DBC=S△DBM时
∴△DBC与△DBM是等高的三角形
∴直线BD与直线CM平行
设CM的解析式为y= ![]()
又∵C(2,4)
∴CM的解析式为y=![]()
又∵M(a,1)且在第一象限
∴a=6 .
(3) 由勾股定理得,AB=![]() ,
,
∵点C为边AB的中点,
∴AC=![]() AB=
AB=![]() ×4
×4![]() =2
=2![]() ,AD=5
,AD=5
∴CD=![]()
设E(0,x),则DE=∣x-3 ∣,D(0,x)
①DC=DE时,
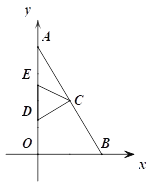
∴![]() =∣x-3 ∣
=∣x-3 ∣
∴x=![]() 或x=
或x=![]()
∴E(0, ![]() )或(0,
)或(0, ![]() );
);
②CE=CD时,过C作CF⊥AO交AO于F,
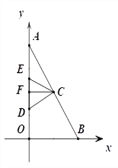
∴F为DE的中点,且F (0,4)
∴EF=DF=1
∴x-4=1
∴x=5
E(0,5)
③ EC=ED时,过E作EQ⊥CD于Q,
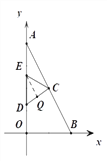
则EQ∥AB,
∴Q为CD的中点,
∴E为AD的中点,
∴AE=ED,
∴8x=x3,
解得:x=![]() ,
,
E(0, ![]() );
);
综上所述:当△CDE为等腰三角形时,E点的坐标为(0, ![]() +3)或(0,
+3)或(0,![]() +3)或(0,5)或(0,
+3)或(0,5)或(0, ![]() ).
).


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:
【题目】将下列各数填在相应的大括号里:
1, —5, ![]() , —4.2, 0,
, —4.2, 0, ![]() , 10,—
, 10,—![]() ,
,
整数:{ … }
非负整数:{ … }
分数:{ … }
负分数:{ … }
有理数:{ … }
非负有理数:{ … }
查看答案和解析>>
科目:初中数学 来源: 题型:
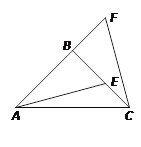
【题目】如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:△ABE≌△CBF;
(2)若![]() ,AE=2,求△ACF的周长.
,AE=2,求△ACF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】满足下列条件的△ABC不是直角三角形的是( )
A. BC=1,AC=2,AB=![]() ; B. BC:AC:AB=3:4:5
; B. BC:AC:AB=3:4:5
C. ∠A+∠B=∠C D. ∠A:∠B:∠C=3:4:5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传节约用水,小明随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如下统计图.
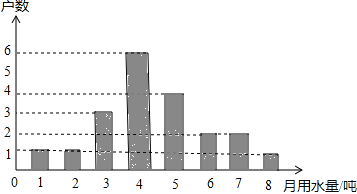
(1)小明一共调查了_____户家庭;所调查家庭5 月份用水量的众数是____;
(2)求所调查家庭5 月份用水量的平均数;
(3)若该小区有400 户居民,请你估计这个小区5 月份的用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用代数式表示.
(1)“x的5倍与y的和的一半”可以表示为_____.
(2)南平乡有水稻田m亩,计划每亩施肥a千克;有玉米田n亩,计划每亩施肥b千克,共施肥_____千克.
(3)有三个连续的整数,最小数是m,则其他两个数分别是_____和_____.
(4)全班总人数为y,其中男生占56%,那么女生人数是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com