

分析 (1)根据翻折的性质,可得D′C的长,根据锐角三角函数,可得BC的长,根据有理数的减法,可得答案;根据三角形外角的性质,可得答案;
(2)根据相似三角形的性质,可得答案;
(3)根据等腰三角形的判定,可得答案.
解答 解:(1)由翻折的性质,得
D′C=$\sqrt{3}$,
由∠A=30°,AC=$\sqrt{3}$,
tan∠A=$\frac{BC}{AC}$=$\frac{BC}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
BC=1,
BD′=CD′-BC=$\sqrt{3}$-1,
由三角形外角的性质,得
∠D′+∠BFD′=∠ABC=60°,
∠BFD′=60°-∠D′=60°-30°=30°;
(2)设平移的距离CC′为x,BC′=1-x,
由△BC′E′∽△BCA,得
$\frac{BC′}{BC}$=$\frac{E′C′}{AC}$,即$\frac{1-x}{1}$=$\frac{1}{\sqrt{3}}$,
解得x=1-$\frac{\sqrt{3}}{3}$;
(3)∠DCM=∠D=30°,△CDM为等腰三角形,即旋转角为∠DCM=30°,
∠DCM=∠DMC=$\frac{180°-∠D}{2}$=75°,△CDM为等腰三角形,即旋转角为∠DCM=75°,
故答案为:$\sqrt{3}$-1,30;1-$\frac{\sqrt{3}}{3}$;30°或75°.
点评 本题考查了翻折的性质,(1)利用了翻折的性质,锐角三角函数,三角形外角的性质;(2)利用了相似三角形的性质;(3)利用了等腰三角形的判定,分类讨论是解题关键,以防遗漏.


科目:初中数学 来源: 题型:解答题
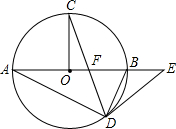 如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有点E,且EF=ED.
如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有点E,且EF=ED.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=1,b=2,c=3 | B. | a=2,b=3,c=4 | C. | a=2,b=4,c=5 | D. | a=3,b=4,c=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
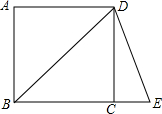 如图,正方形ABCD中,AB=$\sqrt{3}$,延长BC至E,使BE=BD,则△BDE的面积为$\frac{3}{2}$$\sqrt{2}$.
如图,正方形ABCD中,AB=$\sqrt{3}$,延长BC至E,使BE=BD,则△BDE的面积为$\frac{3}{2}$$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
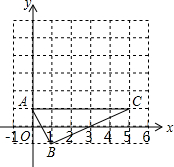 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1).
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com