
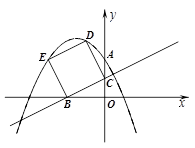
 个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在y轴上时,正方形和抛物线均停止运动.
个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在y轴上时,正方形和抛物线均停止运动.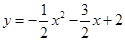 ;
; 时,S=5t2,当
时,S=5t2,当 <t≤1时,S=5t﹣
<t≤1时,S=5t﹣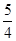 ,当1<t≤
,当1<t≤ 时,S=﹣5t2+15t﹣
时,S=﹣5t2+15t﹣ ;②运动停止时,抛物线的顶点坐标为(
;②运动停止时,抛物线的顶点坐标为( ,
,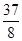 ).
). 秒,期间可以划分成三个阶段:当0<t≤
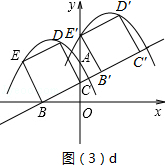
秒,期间可以划分成三个阶段:当0<t≤ 时,对应图(3)a;当
时,对应图(3)a;当 <t≤1时,对应图(3)b;当1<t≤
<t≤1时,对应图(3)b;当1<t≤ 时,对应图(3)c.每个阶段的表达式不同,请对照图形认真思考;
时,对应图(3)c.每个阶段的表达式不同,请对照图形认真思考; ),可知整条抛物线向右平移了3个单位,向上平移了
),可知整条抛物线向右平移了3个单位,向上平移了 个单位.由此得到平移之后的抛物线解析式,进而求出其顶点坐标.
个单位.由此得到平移之后的抛物线解析式,进而求出其顶点坐标.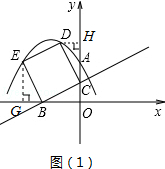
 ,解得
,解得 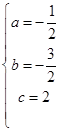 ,
,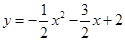 ;
; .
. 时,如图(3)a所示.
时,如图(3)a所示.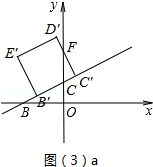
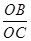 =2,又∵∠BCO=∠FCC′
=2,又∵∠BCO=∠FCC′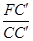 =2
=2 t,∴FC′=2
t,∴FC′=2 t.
t. CC′•FC′=
CC′•FC′=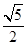 t×
t×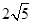 t=5t2
t=5t2 <t≤1时,如图(3)b所示.
<t≤1时,如图(3)b所示.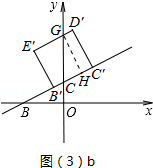

 ,∴CH=
,∴CH= GH=
GH=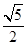
 t,∴HC′=
t,∴HC′= t﹣
t﹣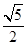 ,∴GD′=
,∴GD′= t﹣
t﹣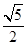
 (
( t﹣
t﹣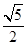 +
+ t)
t) =5t﹣
=5t﹣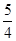
 .
. 时,如图(3)c所示
时,如图(3)c所示
 t,B′C′=
t,B′C′= ,
, t﹣
t﹣ ,∴B′N=2CB′=
,∴B′N=2CB′=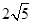 t﹣
t﹣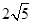
 ,∴E′N=B′E′﹣B′N=
,∴E′N=B′E′﹣B′N=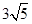 ﹣
﹣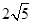 t
t E′N=
E′N= (
(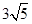 ﹣
﹣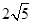 t)
t) (
(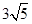 ﹣
﹣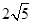 t)•
t)• (
(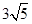 ﹣
﹣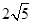 t)=5t2﹣15t+
t)=5t2﹣15t+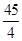
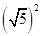 ﹣(5t2﹣15t+
﹣(5t2﹣15t+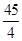 )=﹣5t2+15t﹣
)=﹣5t2+15t﹣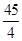
 时,S=5t2,
时,S=5t2, <t≤1时,S=5t﹣
<t≤1时,S=5t﹣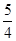 ,
, 时,S=﹣5t2+15t﹣
时,S=﹣5t2+15t﹣ ;
;


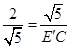
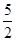
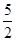 =
=
 )
) ),可知整条抛物线向右平移了3个单位,向上平移了
),可知整条抛物线向右平移了3个单位,向上平移了 个单位.
个单位.
 ,
, )
) ,
,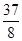 ).
).

 口算能手系列答案
口算能手系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com