
【题目】记多项式x2+2x+1为 f(x),多项式y2-4y+4为f(y),且多项式f(x)的项数为a,f(y)的次数、一次项系数分别是b、m,数a,b,m数轴上分别对应着点A,B,M.
(1)求代数式a2-b2的值;
(2)数轴上有一点G,且到点M,B的距离相等.
①求线段GA的长;
②若n是关于x的方程mx+b=ax的解,且数轴上点N对应着数n,比较线段NG与NB的大小.
【答案】(1)5;(2)①线段GA的长为4;②NB>NG.
【解析】
(1)根据多项式的项数、次数的定义得到a,b的值,然后代入求值;
(2)首先求出点G表示的数,然后再求线段GA的长;
(3)将a=3,b=2,m=-4代入方程并求解,即可得到数轴上点N对应的数n,然后分别计算出线段NG和线段NB的长,比较即可.
解:(1)由题意可得:a=3,b=2,m=-4,
∴a2-b2=9-4=5;
(2)①∵点G到点M,B的距离相等,
∴点G表示的数为:![]() ,
,
∴线段GA的长为:3-(-1)=4;
②由题意可知,该方程为:-4x+2=3x,
解得:![]() ,即数轴上点N对应的数n
,即数轴上点N对应的数n![]() ,
,
∴线段NG的长为:![]() ,
,
线段NB的长为:![]() ,
,
∴NB>NG.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() (x+1)(x﹣3)与x轴交于A、B两点,与y轴交于点C,点D为该抛物线的对称轴上一点,当点D到直线BC和到x轴的距离相等时,则点D的坐标为 .
(x+1)(x﹣3)与x轴交于A、B两点,与y轴交于点C,点D为该抛物线的对称轴上一点,当点D到直线BC和到x轴的距离相等时,则点D的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
⑴ac<0;
⑵当x>1时,y的值随x值的增大而减小.
⑶3是方程ax2+(b﹣1)x+c=0的一个根;
⑷当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为()
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线与x轴的一个交点坐标为(﹣2,0) B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0 D. 抛物线在对称轴左侧部分是上升的
查看答案和解析>>
科目:初中数学 来源: 题型:
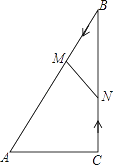
【题目】如图,在![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发, 在
出发, 在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,设运动时间为
匀速运动,设运动时间为![]() 秒
秒![]() ,连接
,连接![]() .
.
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若
若![]() 与
与![]() 相似,求
相似,求![]() 的值;
的值;
![]() 当
当![]() 为何值时,四边形
为何值时,四边形![]() 的面积为
的面积为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22019的值.
解:设S=1+2+22+23+24+…+22019,将等式两边同时乘以2得:2S=2+22+23+24+25+…+22019+22020
将下式减去上式得2S-S=22020-1
即S=22020-1
即1+2+22+23+24+…=22020-1
请你仿照此法计算:
(1)1+2+22+23+24+…+220
(2)1+5+52+53+54+…+5n(其中n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自主学习,请阅读下列解题过程.
解一元二次不等式:x2﹣5x>0.
解:设x2﹣5x=0,解得:x1=0,x2=5,则抛物线y=x2﹣5x与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=x2﹣5x的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即x2﹣5x>0,所以,一元二次不等式x2﹣5x>0的解集为:x<0,或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的 和 .(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式x2﹣5x<0的解集为 .
(3)用类似的方法解一元二次不等式:x2﹣2x﹣3>0.
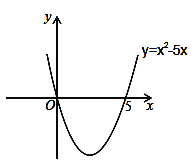
查看答案和解析>>
科目:初中数学 来源: 题型:
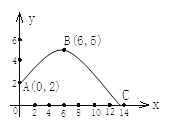
【题目】在体育测试时,初三的一名高个子男生推铅球,已知铅球所经过的路线是某二次函数图象的一部分(如图),若这个男生出手处A点的坐标为(0,2),铅球路线的最高处B点的坐标为B(6,5).
(1)求这个二次函数的表达式;
(2)该男生把铅球推出去多远?(精确到0.01米).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com