
【题目】如图1,在平面直角坐标系中,![]() ,
,![]() 在
在![]() 轴上,
轴上,![]() 在
在![]() 轴上,
轴上,![]() .
.
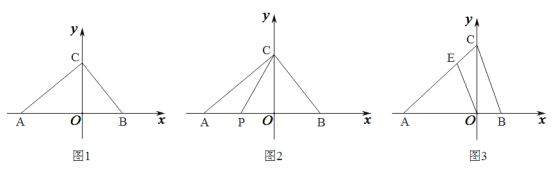
(1)求证:![]() ;
;
(2)如图2,若点![]() ,
,![]() ,现有一个动点
,现有一个动点![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 轴正方向运动,连结
轴正方向运动,连结![]() ,当
,当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标;
的坐标;
(3)如图3,若![]() ,点
,点![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,求
,求![]() 的长.
的长.
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADC都是等边三角形,点E,F同时分别从点B,A出发,以相同的速度各自沿BA,AD的方向运动到点A,D停止,连结EC,FC.

(1)在点E,F运动的过程中,∠ECF的大小是否随之变化?请说明理由.
(2)在点E,F运动的过程中,以A,E,C,F为顶点的四边形的面积变化了吗?请说明理由.
(3)连结EF,在图中找出所有和∠ACE相等的角,并说明理由.
(4)若点E,F在射线BA,射线AD上继续运动下去,(1)中的结论还成立吗?直接写出结论,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
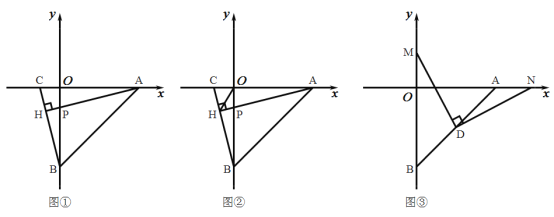
【题目】如图所示,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)如图①,若![]() 的坐标为
的坐标为![]() ,且
,且![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,试求点
,试求点![]() 的坐标;
的坐标;
(2)如图②,在(I)的条件下,连接![]() ,求
,求![]() 的度数;
的度数;
(3)如图③,若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 轴正半轴上一动点,连接
轴正半轴上一动点,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 轴于
轴于![]() 点,当
点,当![]() 点在
点在![]() 轴正半轴上运动的过程中,式子
轴正半轴上运动的过程中,式子![]() 的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.
的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市文化宫学习十九大有关优先发展教育的精神,举办了为某贫困山区小学捐赠书包活动.首次用2000元在商店购进一批学生书包,活动进行后发现书包数量不够,又购进第二批同样的书包,所购数量是第一批数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)求文化官第一批购进书包的单价是多少?
(2)商店两批书包每个的进价分别是68元和70元,这两批书包全部售给文化宫后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
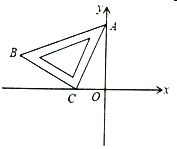
【题目】如图,将一块等腰直角三角板![]() 放置在平面直角坐标系中,
放置在平面直角坐标系中,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的负半轴上,点
轴的负半轴上,点![]() 在第二象限,
在第二象限,![]() 所在直线的函数表达式是
所在直线的函数表达式是![]() ,若保持
,若保持![]() 的长不变,当点
的长不变,当点![]() 在
在![]() 轴的正半轴滑动,点
轴的正半轴滑动,点![]() 随之在
随之在![]() 轴的负半轴上滑动,则在滑动过程中,点
轴的负半轴上滑动,则在滑动过程中,点![]() 与原点
与原点![]() 的最大距离是__________.
的最大距离是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣(x﹣a)(x﹣b),其中a<b,m、n(m<n)是方程1﹣(x﹣a)(x﹣b)=0的两个根,则实数a、b、m、n的大小关系是( )
A. a<m<n<b B. m<a<b<n C. a<m<b<n D. m<a<n<b
查看答案和解析>>
科目:初中数学 来源: 题型:
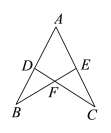
【题目】如图,D,E分别是AB,AC上的点,BE与CD交于点F,给出下列三个条件:①∠DBF=∠ECF;②∠BDF=∠CEF; ③BD=CE.两两组合在一起,共有三种组合:(1)①②;(2)①③;(3)②③问能判定AB=AC的组合的是( )
A.(1)(2)B.(1)(3)C.(2)(3)D.(1)(2)(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】信息1:我们已经学完了解分式方程,它的一般步骤为:确定最简公分母、化为整式方程、求出整式方程的解、进行检验(第一,代入最简公分母验证是否为零,第二代入分式方程的左右两边检验是否相等)、确定分式方程的解.其中代入最简公分母验证这一步也就是在验证所有分式在取此值时是否有意义;
信息2:遇到![]() 这种特征的题目,可以两边同时平方得到
这种特征的题目,可以两边同时平方得到![]() ;
;
信息3:遇到![]() 这种特征的题目,可以将左边变形,得到
这种特征的题目,可以将左边变形,得到![]() ,进而可以得到
,进而可以得到![]() 或
或![]() .
.
结合上述信息解决下面的问题:
问题1:如果![]() .可得:
.可得:![]() ;
;
问题2:解关于b的方程:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com