
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,
上,![]() ,连结
,连结![]() ,点
,点![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 的中点.
的中点.
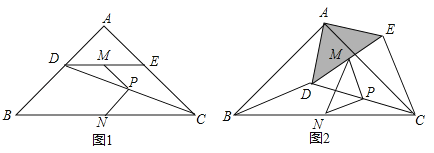
(1)观察猜想图1中,线段![]() 与
与![]() 的数量关系是_______,位置关系是_______;
的数量关系是_______,位置关系是_______;
(2)探究证明把![]() 绕点
绕点![]() 逆时针方向旋转到图2的位置,连结
逆时针方向旋转到图2的位置,连结![]() 、
、![]() 、
、![]() ,判断
,判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)拓展延伸把![]() 绕点
绕点![]() 在平面内自由旋转,若
在平面内自由旋转,若![]() ,
,![]() ,请直接写出
,请直接写出![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 是等腰直角三角形,理由见解析;(3)
是等腰直角三角形,理由见解析;(3)![]() 面积的最大值为
面积的最大值为![]() .
.
【解析】
(1)利用三角形的中位线得出PM=![]() CE,PN=
CE,PN=![]() BD,进而判断出BD=CE,即可得出结论,再利用三角形的中位线得出
BD,进而判断出BD=CE,即可得出结论,再利用三角形的中位线得出![]() 得出
得出![]() ,最后用互余即可得出结论;
,最后用互余即可得出结论;
(2)先判断出![]() ,得出
,得出![]() ,同(1)的方法得出
,同(1)的方法得出![]() ,
,![]() ,即可得出
,即可得出![]() ,同(1)的方法即可得出结论;
,同(1)的方法即可得出结论;
(3)先判断出![]() 最大时,
最大时,![]() 的面积最大,进而求出
的面积最大,进而求出![]() ,
,![]() ,即可得出
,即可得出![]() ,最后用面积公式即可得出结论.
,最后用面积公式即可得出结论.
解:(1)∵点![]() 、
、![]() 是
是![]() 、
、![]() 的中点
的中点
∴![]() ,
,![]()
∵点![]() 、
、![]() 是
是![]() 、
、![]() 的中点
的中点
∴![]() ,
,![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
(2)结论:![]() 是等腰直角三角形.
是等腰直角三角形.
证明:由旋转知,![]()
∵![]() ,
,![]()
∴![]()
∴![]() ,
,![]()
∵由三角形中位线的性质可知,![]() ,
,![]()
∴![]()
∴![]() 是等腰三角形
是等腰三角形
∵同(1)的方法得,![]() 、
、![]()
同(1)的方法得, ![]() 、
、![]()
∴![]()
∴![]()
![]()
![]()
![]()
![]()
![]()
∵![]()
∴![]()
∴![]()
∴![]() 是等腰直角三角形;
是等腰直角三角形;
(3)∵由(2)得,![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() 最大时,
最大时,![]() 的面积最大
的面积最大
∴![]() 且
且![]() 在顶点
在顶点![]() 上面时,
上面时,![]() ,连接AM,AN,如图:
,连接AM,AN,如图:
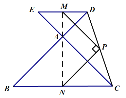
∵在![]() 中,
中,![]() ,
,![]()
∴![]()
∵在![]() 中,
中,![]() ,
,![]()
∴![]()
∴![]()
∴![]() .
.
故答案是:(1)![]() ,
,![]() ;(2)
;(2)![]() 是等腰直角三角形,理由见解析;(3)
是等腰直角三角形,理由见解析;(3)![]() 面积的最大值为
面积的最大值为![]()


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
销售额 |
|
|
|
|
|
|
|
频数 | 7 | 9 | 3 |
| 2 |
| 2 |
数据分析表
平均数 | 众数 | 中位数 |
20.3 |
| 18 |
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AE是BC边上的高线,BM平分∠ABC交AE于点M,经过B,M 两点的⊙O交BC于点G,交AB于点F ,FB为⊙O的直径.
(1)求证:AM是⊙O的切线
(2)当BE=3,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
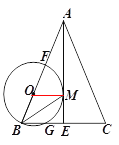
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高淳固城湖大桥采用H型塔型斜拉桥结构(如甲图),图乙是从图甲抽象出的平面图.测得拉索AB与水平桥面的夹角是45°,拉索CD与水平桥面的夹角是65°,两拉索顶端的距离AC为2米,两拉索底端距离BD为10米,请求出立柱AH的长(结果精确到0.1米).

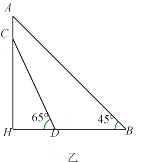
(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上,下列结论:①CE=CF;②BD=1+![]() ;③BE+DF=EF;④∠AEB=75°.其中正确的序号是______.
;③BE+DF=EF;④∠AEB=75°.其中正确的序号是______.
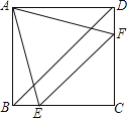
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学共有3个一样规模的大餐厅和2个一样规模的小餐厅,经过测试同时开放2个大餐厅和1个小餐厅,可供3000名学生就餐;同时开放1个大餐厅,1个小餐厅,可供1700名学生就餐.
(1)请问1个大餐厅、1个小餐厅分别可供多少名学生就餐.
(2)如果3个大餐厅和2个小餐厅全部开放,那么能否供全校4500名学生就餐?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在艺术节宣传活动中,采用了四种宣传形式:A唱歌、B舞蹈、C朗诵、D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:

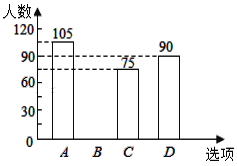
请结合统计图表,回答下列问题:
(1)本次调查的学生共____人,a=______, 并将条形统计图补充完整;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式有一种是“唱歌”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数![]() 的图象G经过点
的图象G经过点![]() ,直线
,直线![]() 与y轴交于点B,与图象G交于点C.
与y轴交于点B,与图象G交于点C.
(1)求m的值.
(2)横、纵坐标都是整数的点叫做整点.记图象G在点A,C之间的部分与线段BA,BC围成的区域(不含边界)为W.
①当直线l过点![]() 时,直接写出区域W内的整点个数.
时,直接写出区域W内的整点个数.
②若区域W内的整点不少于4个,结合函数图象,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com