练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    计算：
    a2-9
    a2-6x+9
    ÷(1+
    3
    a
    )    ．
    考点：分式的混合运算
    专题：
    分析：对第一个分式进行化简，括号内的式子通分相加，然后把除法转化成乘法运算，进行乘除的运算即可求解．
    解答：解：原式=
    (a+3)(a-3)
    (a-3)2
    ÷
    a+3
    a

    =
    a+3
    a-3
    •
    a
    a+3

    =
    a
    a-3
    ．
    点评：本题主要考查分式的混合运算，把分式化到最简是解答的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    计算52012•（-0.2）2013=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    直线y=-2x+6与两坐标轴围成的三角形面积是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

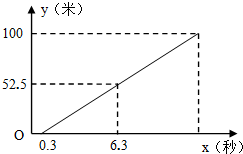    为弘扬体育精神，锻炼师生体魄，我校组织了今年春季运动会．在男子100米预赛中，高二年级某同学甲在发令枪响的同时立即起跑，起跑后甲与起点的距离与甲起跑后的时间大致满足正比例函数的关系．如果用y（米）表示与起点的距离，用x（秒）表示起跑后的时间，测得两个瞬间的x、y如下表：
    起跑后的时间x（秒） 3 9
    与起跑点距离y（米） 24 72
    （1）求同学甲跑动过程中的函数关系式，并写出x的取值范围？
    （2）如果同组另一位同学乙在发令枪响后与起点的距离与发令枪响后的时间大致满足下面的图象，请问：同学乙能否超越同学甲？若能，请通过计算求出在何时超越？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：
    （1）（3a2）3•4b3÷（6ab）2
    （2）先化简，再求值：（x+2）（x-2）-x（2x-1）+（x-1）2，其中x=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系中，A点在x轴的正半轴上，C点在y轴的正半轴上，矩形OABC的顶点B在第一象限内，D点在AB边上，BD=3AD，连接OB，作直线CD，又知OB=10，tan∠AOB=
    4
    3
    ．
    （1）求直线CD的解析式；
    （2）动点P从O点出发，沿OA以每秒2个单位长的速度向终点A匀速运动，同时，动点Q从A点出发，沿AB以每秒1个单位长的速度匀速运动到D点后，又以每秒6个单位长的速度继续向终点B匀速运动．连接PQ、OQ，设P、Q运动的时间为t（秒），△POQ的面积为S（平方单位），求S与t之间的函数关系式，并直接写出自变量t的取值范围；
    （3）在（2）的条件下，连接CP、CQ，问是否存在这样的t值，使得∠OPC=∠OQC？若存在，请求出所有满足条件的t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    若实数x≠y，且满足（x+1）2+2（x+1）-2=0，y2+4y+1=0．则x
    y
    x
    +y
    x
    y
    =（　　）
    A、2B、4C、±2D、-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    二次函数y=x2+bx+c中，则b+c=0，则它的图象必经过下列四点中的（　　）
    A、（1，1）
    B、（1，-1）
    C、（-1，-1）
    D、（-1，1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解方程：
    （1）9x2=16
    （2）（1-2x）3=-125．

    查看答案和解析>>

    同步练习册答案