

分析 (1)由角平分线的定义可知∠MOB=$\frac{1}{2}$∠AOB,∠BON=$\frac{1}{2}$∠BOD,然后依据∠MON=∠MOB+∠BON求解即可;
(2)由角平分线的定义可知∠MOC=$\frac{1}{2}$∠AOC,∠BON=$\frac{1}{2}$∠BOD.,接下来依据∠MON=∠MOC+∠BON-∠BOC计算即可.
解答 解:(1)∵OM平分∠AOB,ON平分∠BOD,
∴∠MOB=$\frac{1}{2}$∠AOB,∠BON=$\frac{1}{2}$∠BOD.
∴∠MON=∠MOB+∠BON=$\frac{1}{2}$∠AOB+$\frac{1}{2}$∠BOD=$\frac{1}{2}$(∠AOB+∠BOD)=$\frac{1}{2}$×160°=80°.
(2)∵OM平分∠AOC,ON平分∠BOD,
∴∠∠MOC=$\frac{1}{2}$∠AOC,∠BON=$\frac{1}{2}$∠BOD.
∴∠MON=∠MOC+∠BON-∠BOC=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOD-∠BOC
=$\frac{1}{2}$(∠AOC+∠BOD)-∠BOC
=$\frac{1}{2}$×180°-20°=70°
点评 本题主要考查的是角平分线的定义、角的和差计算,掌握图形间相关角之间的关系是解题的关键.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD≠BC,AD∥BC,∠B=70°,∠C=40°,画出线段CD平移后的线段,其平移的方向为射线CB的方向,平移的距离为线段AD的长,平移后所得的线段与BC相交于点E,
如图,在四边形ABCD中,AD≠BC,AD∥BC,∠B=70°,∠C=40°,画出线段CD平移后的线段,其平移的方向为射线CB的方向,平移的距离为线段AD的长,平移后所得的线段与BC相交于点E,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,三角形ABC沿BC边所在的直线向左平移得到三角形DEF,下列说法错误的是( )
如图,三角形ABC沿BC边所在的直线向左平移得到三角形DEF,下列说法错误的是( )| A. | DE∥AB | B. | ∠D=∠A | C. | AC=DF | D. | ∠D=∠DEF |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,点A的坐标为A(0,a),将点A向右平移b个单位得到点B,其中a,b满足:(3a-2b)2+|a+b-5|=0.
如图所示,点A的坐标为A(0,a),将点A向右平移b个单位得到点B,其中a,b满足:(3a-2b)2+|a+b-5|=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 过平行四边形纸片的一个顶点作一条线段,沿这条线段剪下一个三角形纸片,将它平移到右边的位置,可得到新的平行四边形.
过平行四边形纸片的一个顶点作一条线段,沿这条线段剪下一个三角形纸片,将它平移到右边的位置,可得到新的平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
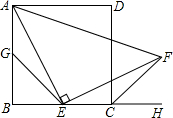 如图所示,四边形ABCD是正方形,点E是边BC的中点且∠AEF=90°,EF交正方形外角平分线CF于点F,取边AB的中点G,连接EG.
如图所示,四边形ABCD是正方形,点E是边BC的中点且∠AEF=90°,EF交正方形外角平分线CF于点F,取边AB的中点G,连接EG.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 周长相等的锐角三角形都全等 | B. | 周长相等的直角三角形都全等 | ||
| C. | 周长相等的钝角三角形都全等 | D. | 周长相等的等边三角形都全等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com