
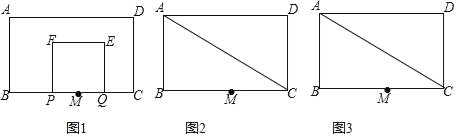
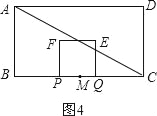
����Ŀ����ͼ���ھ���ABCD�У�AB=3��BC=4����M��BC���е㣬��P�ӵ�M������MB��ÿ��1����λ���ٶ����B�����˶��������B��������ԭ�ٶ���BM���أ�ͬʱ��Q�ӵ�M������ÿ��1����λ�����ٶ�������MC�������˶����ڵ�P��Q���˶������У���PQΪ����������PQEF��ʹ�������ABCD��BC��ͬ�࣬��P��Qͬʱ����������P���ص�Mʱ��������ֹͣ�˶������P��Q�˶���ʱ����t�루t��0����
��1������P�˶���BM���е�ʱ��t=�� ����
��2����������PQEF�����ABCD�ص����ֵ����ΪS��ֱ��д��S��t֮��ĺ�����ϵʽ��t��ȡֵ��Χ��
��3������AC����������PQEF����ADC�ص�����Ϊ������ʱ����t��ȡֵ��Χ��
���𰸡���1��1��3����2����S=4t2����S=6t����S=��3t+18����3��![]() ��t��
��t��![]() ��t=2
��t=2
����������������1�����BM=![]() BC=2������P��һ���˶���BM���е�ʱ��PM=
BC=2������P��һ���˶���BM���е�ʱ��PM=![]() BM=1���ó�t=1������P�ڶ����˶���BM���е�ʱ���˶���·��=3���ó�t=3���ɣ�
BM=1���ó�t=1������P�ڶ����˶���BM���е�ʱ���˶���·��=3���ó�t=3���ɣ�
��2����Ϊ����������ٵ�0<t��1.5ʱ��PQ=2t���������������ʽ���ɵó��𰸣�
�ڵ�1.5<t��2ʱ�ó�PQ=2t��AB=3���ɾ���������ɵó��𰸣�
�۵�2<t��4ʱ�����PC=6-t��AB=3���ɾ���������ɵó��𰸣�
��3������E��AC��ʱ���ó���CEQ�ס�CAB���ó���Ӧ�߳ɱ��������ɵó�t��ֵ����F��AC��ʱ����CPF�ס�CBA���ó���Ӧ�߳ɱ��������ɵó�t��ֵ������F��EA���ӳ�����ʱ����E��CD���ӳ����ϣ���ʱt=2�����ɵó��𰸣�
��⣺��1����BC=4����M��BC���е㣬
��BM=![]() BC=2��
BC=2��
����P��һ���˶���BM���е�ʱ��PM=![]() BM=1��
BM=1��
��t=1��
����P�ڶ����˶���BM���е�ʱ���˶���·��=2+1=3��
��t=3��
�ʴ�Ϊ��1��3��
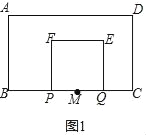
��2�������������
����ͼ1����0��t��1.5ʱ��
��PQ=2t��
��S=��2t��2��
��S=4t2��
����ͼ2��
��1.5��t��2ʱ��
��PQ=2t��AB=3��
��S=6t��
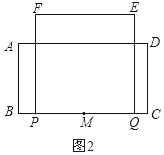
����ͼ3��
��2��t��4ʱ��
��PC=6��t��AB=3��
��S=��3t+18��
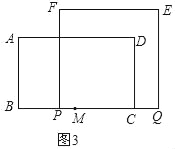
��3����ͼ4��
����E��AC��ʱ��
�ߡ�CEQ�ס�CAB��
��![]() ��
��
��![]() ��
��
��t=![]() ��
��
��F��AC��ʱ��
�ߡ�CPF�ס�CBA��
��![]() ��
��
��![]() ��
��
��t=![]() ������F��EA���ӳ�����ʱ����E��CD���ӳ����ϣ���ʱt=2��
������F��EA���ӳ�����ʱ����E��CD���ӳ����ϣ���ʱt=2��
��t��ȡֵ��Χ��![]() ��t��
��t��![]() ��t=2��
��t=2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() �ֱ���
�ֱ���![]() �ᣬ
�ᣬ![]() �ύ��
�ύ��![]() ���㣬��ֱ��
���㣬��ֱ��![]() ���ڵ�
���ڵ�![]() .
.
��1����![]() ������Ϊ__________����
������Ϊ__________����![]() ������Ϊ__________
������Ϊ__________
��2�����߶�![]() ����һ��
����һ��![]() ������
������![]() ��
��![]() ���ƽ����
���ƽ����![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() �����
�����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ����
����![]() Ϊ��ֵʱ���ı���
Ϊ��ֵʱ���ı���![]() ��ƽ���ı���.
��ƽ���ı���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0���Ĵ���ͼ����ͼ��ʾ�����ڸö��κ���������˵���д�����ǣ�������
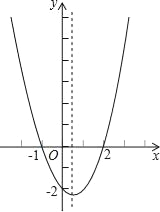
A. ��������Сֵ B. �Գ�����ֱ��x=![]()
C. ����1��x��2ʱ��y��0 D. ��x��![]() ʱ��y��x�����������
ʱ��y��x�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��ֽƬ���۵���ʹ��B��AD���ϵĵ�K�غϣ�EGΪ�ۺۣ���C��AD���ϵĵ�K�غϣ�FHΪ�ۺۣ���֪��1=67.5�㣬��2=75�㣬EF=![]() +1����BC�ij���
+1����BC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
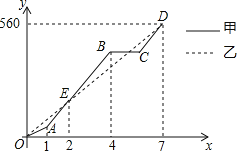
����Ŀ��������ڼ䣬�ס���������ͬһ·����ʻ�����Կ���ͬʱȥ���560ǧ�ľ������棬������ÿСʱ60ǧ���ٶ�������ʻ1Сʱ������ÿСʱmǧ���ٶ�������ʻ��;����Ϣ��һ��ʱ�������ÿСʱmǧ���ٶ�������ʻ������ͬʱ����Ŀ�ĵأ�ͼ�����ߡ��߶ηֱ��ʾ�ס����������ߵ�·��![]() ��
��![]() ��ʱ��
��ʱ��![]() ֮��ĺ�����ϵ��ͼ��
֮��ĺ�����ϵ��ͼ��![]() �����ͼ���ṩ����Ϣ������������⣺
�����ͼ���ṩ����Ϣ������������⣺
![]() ͼ��E���������______������
ͼ��E���������______������![]() ______
______![]() ������;����Ϣ______h��
������;����Ϣ______h��
![]() ���߶�CD�Ľ���ʽ����д���Ա���x��ȡֵ��Χ��
���߶�CD�Ľ���ʽ����д���Ա���x��ȡֵ��Χ��
![]() ���˵ڶ����������־����ʱ���������20km��
���˵ڶ����������־����ʱ���������20km��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
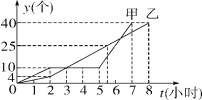
����Ŀ��ij����ļס����������˷ֱ�ͬʱ����ͬ�����������һ���������y(��)������ʱ��t(Сʱ)�Ĺ�ϵ��ͼ��ʾ��
(1)����ͼ��ش�
�ټס����У�˭�����һ����������������������У�˭���������ֹͣ��������Сʱ��
�ڵ�t���ڶ���ʱ���ס��������������������ȣ�
(2)˭����һ��ʱ���ڵ������ٶ���죿��ö�ʱ���ڣ���ÿСʱ��������ĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��D��E�ֱ�����ABC�ı�BA��BC�ӳ����ϵĵ㣬����DAC��ƽ����AF����AF��BC��

��1����֤����ABC�ǵ��������Σ�
��2������ACE��ƽ���߽�AF�ڵ�G������B��40�������AGC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ����.
��1��ij��ҩ������һ��ҩƷ�����þɹ��գ����ˮ����Ҫ�Ȼ������Ƶ����������200t��������¹��գ����ˮ�����Ȼ������Ƶ��������100t���¡��ɹ��յķ�ˮ����֮��Ϊ2��5�����ֹ��յķ�ˮ�������Ƕ��٣�
��2��Ԫ���ڼ䣬�����ݳ����麣��������ۣ�ȥʱ�ڸ���Ĵ���������60���ӣ�����ʱƽ���ٶ������5ǧ��/Сʱ���ڸ���Ĵ����ϵ���ʱ��ȥʱ������5���ӣ������Ĵ��ŵij���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���ABCD�ĶԽ���AC��BD���ڵ�O�����������ĸ��۶ϣ�
��OA=OC����AB=CD���ۡ�BAD=��DCB����AD��BC��
�������ѡ�������۶���Ϊ�����������ı���ABCDΪƽ���ı�������Ϊ���ۣ�������и��⣺
��1������һ�������⣬��ͼ������֤����
��2������һ�������⣬�ٷ�������˵����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com