

���� ��1�����������߽���ʽ�ɷֱ���a��b��ʾ��A��B��������꣬����BΪOA���е�ɵõ�a��b֮��Ĺ�ϵʽ��
��2���������߽���ʽ�������C�����꣬��C��CD��x���ڵ�D����֤�á�OCD�ס�CAD�������������ε����ʿɵõ�����a�ķ��̣������OA��CD�ij�������á�OAC�������
��3��������OC��l�Ľ��㼴Ϊ���������ĵ�P�������OC�Ľ���ʽ��������P�����ꣻ
�����E�����꣬��ɱ�ʾ����EOB�����������E��x���ƽ���߽�ֱ��BC�ڵ�N���������BC�Ľ���ʽ����ɱ�ʾ��EN�ij�����һ���ɱ�ʾ����EBC���������ɱ�ʾ���ı���OBCE����������ö��κ��������ʿ���������ֵ����E������꣮
��� �⣺
��1����y=x2+ax�У���y=0ʱ��x2+ax=0��x1=0��x2=-a��
��B��-a��0����
��y=-x2+bx�У���y=0ʱ��-x2+bx=0��x1=0��x2=b��
��A��0��b����
��BΪOA���е㣬
��b=-2a��
��$\frac{a}{b}=-\frac{1}{2}$��
��2�������������߽���ʽ�ɵ�$\left\{\begin{array}{l}y={x^2}+ax\\ y=-{x^2}-2ax\end{array}\right.$����ȥy�����ɵ�2x2+3ax=0�����x1=0��${x_2}=-\frac{3}{2}a$��
��$x=-\frac{3}{2}a$ʱ��$y=\frac{3}{4}{a^2}$��
��$C��{-\frac{3}{2}a��\frac{3}{4}{a^2}}��$��
��C��CD��x���ڵ�D����ͼ1��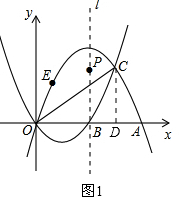
��$D��{-\frac{3}{2}a��0}��$��
�ߡ�OCA=90�㣬
���OCD�ס�CAD��
��$\frac{CD}{AD}=\frac{OD}{CD}$��
��CD2=AD•OD����${��{\frac{3}{4}{a^2}}��^2}=-\frac{1}{2}a•��{-\frac{3}{2}a}��$��
��a1=0����ȥ����${a_2}=\frac{2}{3}\sqrt{3}$����ȥ����${a_3}=-\frac{2}{3}\sqrt{3}$��
��$OA=-2a=\frac{4}{3}\sqrt{3}$��$CD=\frac{3}{4}{a^2}=1$��
��${S_{��OAC}}=\frac{1}{2}OA•CD=\frac{2}{3}\sqrt{3}$��
��3����������${C_2}��y=-{x^2}+\frac{{4\sqrt{3}}}{3}x$��
����Գ���${l_2}��x=\frac{{2\sqrt{3}}}{3}$��
��A����l2�ĶԳƵ�ΪO��0��0����$C��\sqrt{3}��1��$��
��PΪֱ��OC��l2�Ľ��㣬
��OC�Ľ���ʽΪy=kx��
��$1=\sqrt{3}k$����$k=\frac{{\sqrt{3}}}{3}$��
��OC�Ľ���ʽΪ$y=\frac{{\sqrt{3}}}{3}x$��
��$x=\frac{{2\sqrt{3}}}{3}$ʱ��$y=\frac{2}{3}$��
��$P��\frac{{2\sqrt{3}}}{3}��\frac{2}{3}��$��
����$E��m��-{m^2}+\frac{{4\sqrt{3}}}{3}������0��m��\frac{{2\sqrt{3}}}{3}��$��
��${S_{��OBE}}=\frac{1}{2}��\frac{{2\sqrt{3}}}{3}•��-{m^2}+\frac{{4\sqrt{3}}}{3}��=-\frac{{\sqrt{3}}}{3}{m^2}+\frac{4}{3}m$��
��$B��\frac{{2\sqrt{3}}}{3}��0��$��$C��\sqrt{3}��1��$��
��ֱ��BC�Ľ���ʽΪy=kx+b��
��$\left\{{\begin{array}{l}{1=\sqrt{3}k+b}\\{0=\frac{{2\sqrt{3}}}{3}k+b}\end{array}}\right.$�����$k=\sqrt{3}��b=-2$��
��ֱ��BC�Ľ���ʽΪ$y=\sqrt{3}x-2$��
����E��x���ƽ���߽�ֱ��BC�ڵ�N����ͼ2��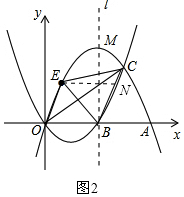
��$-{m^2}+\frac{{4\sqrt{3}}}{3}m=\sqrt{3}x-2$����x=$-\frac{{\sqrt{3}}}{3}{m^2}+\frac{4}{3}m+\frac{{2\sqrt{3}}}{3}$��
��EN=$-\frac{{\sqrt{3}}}{3}{m^2}+\frac{4}{3}m+\frac{{2\sqrt{3}}}{3}-m=-\frac{{\sqrt{3}}}{3}{m^2}+\frac{1}{3}m+\frac{{2\sqrt{3}}}{3}$��
��${S_{��EBC}}=\frac{1}{2}•1•��-\frac{{\sqrt{3}}}{3}{m^2}+\frac{1}{3}m+\frac{{2\sqrt{3}}}{3}��=-\frac{{\sqrt{3}}}{6}{m^2}+\frac{1}{6}m+\frac{{\sqrt{3}}}{3}$
��S�ı���OBCE=S��OBE+S��EBC=$��-\frac{{\sqrt{3}}}{3}{m^2}+\frac{4}{3}m��+��-\frac{{\sqrt{3}}}{6}{m^2}+\frac{1}{6}m+\frac{{\sqrt{3}}}{3}��$=$-\frac{{\sqrt{3}}}{2}{m^2}+\frac{3}{2}m+\frac{{\sqrt{3}}}{3}=-\frac{{\sqrt{3}}}{2}{��m-\frac{{\sqrt{3}}}{2}��^2}+\frac{{17\sqrt{3}}}{24}$��
��$0��m��\frac{{2\sqrt{3}}}{3}$��
�൱$m=\frac{{\sqrt{3}}}{2}$ʱ��${S_{���}}=\frac{{17\sqrt{3}}}{24}$��
��$m=\frac{{\sqrt{3}}}{2}$ʱ��$y=-{��\frac{{\sqrt{3}}}{2}��^2}+\frac{{4\sqrt{3}}}{3}•\frac{{\sqrt{3}}}{2}=\frac{5}{4}$��
��$E��\frac{{\sqrt{3}}}{2}��\frac{5}{4}��$��${S_{���}}=\frac{{17\sqrt{3}}}{24}$��
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ���������������ε��ж������ʡ���ԳƵ����ʡ������ε���������κ��������ʼ�����˼���֪ʶ���ڣ�1���зֱ��ʾ��A��B�������ǽ���Ĺؼ����ڣ�2�������C�����꣬�������������ε��������a��ֵ�ǽ���Ĺؼ����ڣ�3������ȷ����P���λ���ǽ���Ĺؼ����ڣ�3��������E������ֱ��ʾ����OBE�͡�EBC������ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���������ϴ��ѶȽϴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
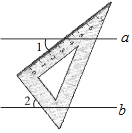 ��ֱ֪��a��b��һ��ֱ�����ǰ���ͼ��ʾ���ã�����1=37�㣬���2�Ķ����ǣ�������
��ֱ֪��a��b��һ��ֱ�����ǰ���ͼ��ʾ���ã�����1=37�㣬���2�Ķ����ǣ�������| A�� | 37�� | B�� | 53�� | C�� | 63�� | D�� | 27�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��A��-1��0����B��4��0����������y=ax2+bx-4��x����������㣬��C����������y��Ľ��㣬����AC�������ߵĶԳ�����x�ύ�ڵ�M��
��ͼ����֪��A��-1��0����B��4��0����������y=ax2+bx-4��x����������㣬��C����������y��Ľ��㣬����AC�������ߵĶԳ�����x�ύ�ڵ�M���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ����ƽ��ֱ������ϵxOy�У�A��4��0����C��0��6������B�ڵ�һ�����ڣ���P��ԭ��O��������ÿ��2����λ���ȵ��ٶ����ų�����OABC�ƶ�һ�ܣ���������O��A��B��C��O��·���ƶ���
��֪����ͼ����ƽ��ֱ������ϵxOy�У�A��4��0����C��0��6������B�ڵ�һ�����ڣ���P��ԭ��O��������ÿ��2����λ���ȵ��ٶ����ų�����OABC�ƶ�һ�ܣ���������O��A��B��C��O��·���ƶ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2•a3=a6 | B�� | ��2ab2��2=4a2b4 | C�� | ��-a2��3=a6 | D�� | 2a2��a=2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
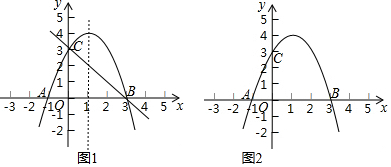
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ھ���ABCD�У�AB��BC��EΪCD�ߵ��е㣬����ADE�Ƶ�E˳ʱ����ת180�㣬��D�Ķ�Ӧ��ΪC����A�Ķ�Ӧ��ΪF������E��ME��AF��BC�ڵ�M������AM��BD���ڵ�N���������н��ۣ�
��ͼ���ھ���ABCD�У�AB��BC��EΪCD�ߵ��е㣬����ADE�Ƶ�E˳ʱ����ת180�㣬��D�Ķ�Ӧ��ΪC����A�Ķ�Ӧ��ΪF������E��ME��AF��BC�ڵ�M������AM��BD���ڵ�N���������н��ۣ�| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com