
| A. | $\left\{{\begin{array}{l}{k=-1}\\{b=1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{k=-1}\\{b=0}\end{array}}\right.$ | C. | $\left\{\begin{array}{l}k=1\\ b=2\end{array}\right.$ | D. | $\left\{\begin{array}{l}k=1\\ b=-4\end{array}\right.$ |
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:解答题
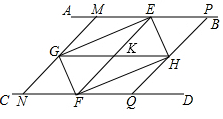 如图,AB∥CD,点E,F分别是AB,CD上,连结EF,∠AEF,∠CFE的平分线交于点G,∠BEF,∠DFE的平分线交于点H.
如图,AB∥CD,点E,F分别是AB,CD上,连结EF,∠AEF,∠CFE的平分线交于点G,∠BEF,∠DFE的平分线交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
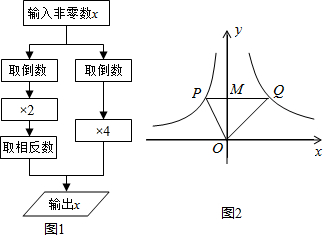
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
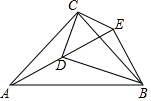 如图,已知△ABC是等腰直角三角形,其内部有一点D,连接BD,以BD为斜边作等腰直角三角形BDE,连接AD、CD、CE,若CD=1,AD=2,∠DCE=90°,则DE的长是 ( )
如图,已知△ABC是等腰直角三角形,其内部有一点D,连接BD,以BD为斜边作等腰直角三角形BDE,连接AD、CD、CE,若CD=1,AD=2,∠DCE=90°,则DE的长是 ( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在圆上 | B. | 在圆内 | C. | 在圆外 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
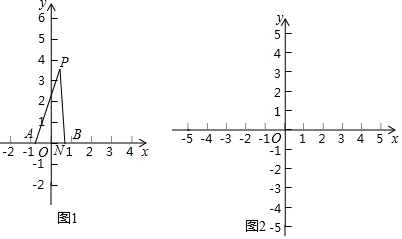
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
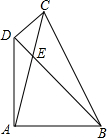 如图,在四边形ABCD中,对角线AC、BD相交于点E,∠DAB=∠CDB=90°,∠ABD=45°,∠DCA=30°,AB=6,则AE=2$\sqrt{6}$.
如图,在四边形ABCD中,对角线AC、BD相交于点E,∠DAB=∠CDB=90°,∠ABD=45°,∠DCA=30°,AB=6,则AE=2$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 40073名学生是总体 | |
| B. | 每名学生是总体的一个个体 | |
| C. | 本次调查是全面调查 | |
| D. | 1000名学生的身高是总体的一个样本 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 随机摸出1个球,是白球 | B. | 随机摸出1个球,是红球 | ||
| C. | 随机摸出1个球,是红球或黄球 | D. | 随机摸出2个球,都是黄球 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com