
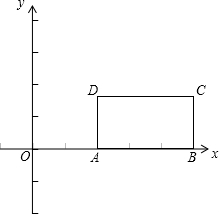
 已知:矩形ABCD(字母顺序如图)的边长AB=3,AD=2,将此矩形放在平面直角坐标系xOy中,使AB在x轴正半轴上,而矩形的其它两个顶点在第一象限,且直线y=
已知:矩形ABCD(字母顺序如图)的边长AB=3,AD=2,将此矩形放在平面直角坐标系xOy中,使AB在x轴正半轴上,而矩形的其它两个顶点在第一象限,且直线y= x-1经过这两个顶点中的一个.
x-1经过这两个顶点中的一个. x-1的上方?还是下方?还是正好落在此直线上?并说明理由.
x-1的上方?还是下方?还是正好落在此直线上?并说明理由.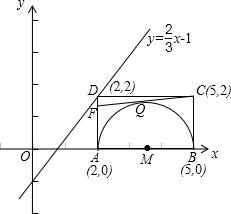 解:(1)如图,建立平面直角坐标系,
解:(1)如图,建立平面直角坐标系, x-1;则2=
x-1;则2= (m+3)-1,
(m+3)-1, x-1;
x-1; x-1,则2=
x-1,则2= m-1,m=2,
m-1,m=2, ,0),
,0),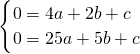 ,
,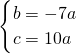 ,
, )2-
)2- a;
a; ,-
,- a)
a) <-
<- a<2,
a<2, <a<-
<a<- .
. ,
, )
) ;
; a=
a= ,
, ;
; x2+
x2+ x-5,
x-5, x-1与y轴交点(0,-1);
x-1与y轴交点(0,-1); x-1下方.
x-1下方. x-1与C点不过y=
x-1与C点不过y= x-1分析,即可求得矩形的顶点A、B、C、D的坐标;
x-1分析,即可求得矩形的顶点A、B、C、D的坐标; x-1下方.
x-1下方.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 已知:矩形ABCD,对角线AC、BD相交于点O.
已知:矩形ABCD,对角线AC、BD相交于点O.| BC |
| CD |
| AO |
| AD |
| AB |
| BC |
| BO |
查看答案和解析>>
科目:初中数学 来源: 题型:
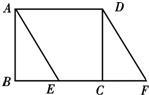 如图,已知在矩形ABCD中,AB=3,点E在BC上且∠BAE=30°,延长BC到点F使CF=BE,连接DF.
如图,已知在矩形ABCD中,AB=3,点E在BC上且∠BAE=30°,延长BC到点F使CF=BE,连接DF.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:矩形ABCD中AD>AB,O是对角线的交点,过O任作一直线分别交BC、AD于点M、N(如图①).
已知:矩形ABCD中AD>AB,O是对角线的交点,过O任作一直线分别交BC、AD于点M、N(如图①).| MN | DN |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 10 | 7 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com