Question

3．已知：点D为正方形ABCD和正方形DEFG的公共顶点，记∠ADG=α，且0°≤α≤180°
（1）当α=0°，即点A在DG边上时，如图，求证：AG=CE且S_△ABG=S_△CBE；
（2）当α≠0°，且A，B，G三点不共线时，如图2，问（1）中的结论是否还成立？若成立，请加以证明；若不成立，请举反例；
（3）已知当α在变化过程中时，△ABG的面积存在最大值，若DA=2，DG=5．请你直接写出△ABG面积的最大值，并画出此时的示意图．

Answer 1

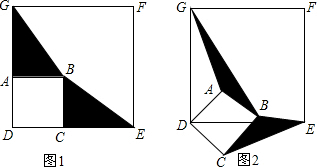
分析 （1）由正方形的性质可知：AD=DC，GD=ED，从而可证明得AG=CE，然后根据AB=BC，AG=CE，根据三角形的面积公式可证得S_△ABG=S_△BCE；
（2）成立，如图2，过点G作GM⊥BA，垂足为M，过点E作EN⊥BC，垂足为N，先证明△GDA≌△EDC得到AG=CE，然后再证明△AGM≌△CEN，得到MG=NE，由三角形的面积公式可知：S_△ABG=S_△BCE；
（3）边长AB不变，所以当BA边上的高线最长时，三角形ABG的面积有最大值，故当α=180°时，三角形ABG的面积最大．

解答 证明：（1）∵四边形ABCD和四边形DEFG均为正方形，
∴AD=DC，AB=BC，GD=ED，∠GAB=∠BCE=90°．
∴GD-AD=ED-DC，即AG=CE．
∵${S}_{△ABG}=\frac{1}{2}AB•AG$，${S}_{△BCE}=\frac{1}{2}BC•CE$，
∴S_△ABG=S_△BCE．
（2）成立．
如图2，过点G作GM⊥BA，垂足为M，过点E作EN⊥BC，垂足为N．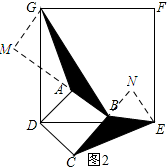

∵∠GDA+∠ADE=90°，∠ADE+∠EDC=90°，
∴∠GAD=∠EDC．
在△GDA和△EDC中，
$\left\{\begin{array}{l}{GD=ED}\\{∠GDA=∠EDC}\\{DA=DC}\end{array}\right.$，
∴△GDA≌△EDC．
∴AG=CE，∠GAD=∠ECD．
∴∠GAD-∠MAD=∠ECD-∠DCB，即∠GAM=∠CEN．
在△AGM和△CEN中，
$\left\{\begin{array}{l}{∠GAM=∠CEN}\\{∠GMA=∠CNE}\\{AG=CE}\end{array}\right.$，
∴△AGM≌△CEN．
∴MG=NE．
∴$\frac{1}{2}AB•MG=\frac{1}{2}BC•EN$，即S_△ABG=S_△BCE．
（3）如图3所示；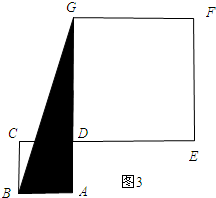

当α=180°时，△ABG的面积有最大值．
${S}_{△ABG}=\frac{1}{2}AB•AG=\frac{1}{2}×2×7$=7．

点评 本题主要考查的是正方形的性质和全等三角形的性质和判定、三角形面积的计算，证得△GDA≌△EDC，△AGM≌△CEN是解题的关键．