
 如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.
如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.分析 (1)根据线段垂直平分线的性质得到FB=FC,根据角平分线的定义得到∠CBA=48°,根据三角形内角和定理计算即可;
(2)根据三角形的面积公式求出DG,根据角平分线的性质解答即可.
解答 解:(1)∵BD平分∠ABC,
∴∠CBA=2∠CBD=2∠ABD=48°,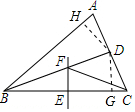
∴∠ACB=180°-60°-48°=72°,
∵EF是BC的中垂线,
∴FB=FC,
∴∠FCB=∠FBC=24°,
∴∠ACF=72°-24°=48°;
(2)作DG⊥BC于G,DH⊥AB于H,
∵BD平分∠ABC,DG⊥BC,DH⊥AB,
∴DH=DG,
∵BF:FD=5:3,S△BCF=10,
∴S△DCF=6,
∴S△BCD=16,
∴DG=$\frac{32}{5}$,
∴DH=DG=$\frac{32}{5}$,即点D到AB的距离为$\frac{32}{5}$.
点评 本题考查的是线段垂直平分线的性质、角平分线的性质,掌握段的垂直平分线上的点到线段的两个端点的距离相等、角的平分线上的点到角的两边的距离相等是今天的关键.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点C在以AB为直径的半圆⊙O上,BE,AD分别为∠ABC,∠CAB的角平分线,AB=6,则DE的长为( )
如图,点C在以AB为直径的半圆⊙O上,BE,AD分别为∠ABC,∠CAB的角平分线,AB=6,则DE的长为( )| A. | 3 | B. | 3$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r,扇形的半径为R,扇形的圆心角等于90°,则R与r之间的关系是R=4r.
如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r,扇形的半径为R,扇形的圆心角等于90°,则R与r之间的关系是R=4r.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点O为平面直角坐标系的原点,点A的坐标为(6,8),点B的坐标为(12,0).
如图,点O为平面直角坐标系的原点,点A的坐标为(6,8),点B的坐标为(12,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,当刻度尺的一边与⊙O相切时,另一边与⊙O的两个交点处的读数如图所示(单位:cm),圆的半径是5,那么刻度尺的宽度为( )
如图,当刻度尺的一边与⊙O相切时,另一边与⊙O的两个交点处的读数如图所示(单位:cm),圆的半径是5,那么刻度尺的宽度为( )| A. | $\frac{25}{6}$cm | B. | 4cm | C. | 3cm | D. | 2cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com