
已知Rt△ABC,∠ACB=90°,AC=BC=4,点O是AB中点,点P、Q分别从点A、C出发,沿AC、CB以每秒1个单位的速度运动,到达点C、B后停止。连结PQ、点D是PQ中点,连结CD并延长交AB于点E.
(1) 试说明:△POQ是等腰直角三角形;
(2) 设点P、Q运动的时间为t秒,试用含t的代数式来表示△CPQ的面积S,并求出
S的最大值;
(3) 如图2,点P在运动过程中,连结EP、EQ,问四边形PEQC是什么四边形,并说明理由;
(4) 求点D运动的路径长(直接写出结果).
 | |||
 | |||
(1)、证明:连接CO,则:CO⊥AB ∠BCO=∠A=45° CO=AO=1/2AB
在△AOP和△COQ中
AP=CQ ,∠A=∠BCO,AO=CO
∴△AOP≌△COQ (SAS)
∴OP=OQ ∴∠AOP=∠COQ
∴∠POQ=∠COQ+∠COP =∠AOP+∠COP=∠AOC =90°
∴△ POQ是等腰直角三角形(3分)
(2)、S=![]() CQ×CP =
CQ×CP =![]() t(4-t) =
t(4-t) =![]() t²+2t =
t²+2t =![]() (t-2)²+2
(t-2)²+2
当t=2时,S取得最大值,最大值S=2 (3分)
(3)、四边形PEQC是矩形
证明:连接OD
∵点D是PQ中点
∴CD=PD=DQ=![]() PQ
PQ
OD=PD=DQ=![]() PQ
PQ
∴CD=OD
∴∠DCO=∠DOC
∵∠CEO+∠DCO=90°
∠DOE+∠DOC=90°
∴∠CEO=∠DOE
∴DE=DO
∴DE=CD
∵PD=DQ
∴四边形PEQC是平行四边形
又∠ACB=90° ∴四边形PEQC是矩形(3分)
(4)、由DO=DC可知:点D在线段OC的垂直平分线上,其运动路径为CO垂直平分线与AC、BC交点间线段
点D运动的路径长=![]() AB=
AB=![]() (3分)
(3分)


科目:初中数学 来源: 题型:
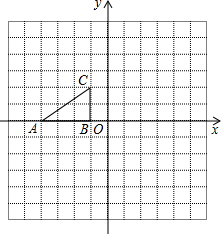 如图,每个小方格都是边长为1个单位的正方形.Rt△ABC 的顶点在格 点上,建立平面直角坐标系后,点A的坐标为(-4,0),点B的坐标为(-1,0).已知Rt△ABC和Rt△A1B1C1关于y轴对称,Rt△A1B1C1和Rt△A2B2C2关于直线y=-2轴对称.
如图,每个小方格都是边长为1个单位的正方形.Rt△ABC 的顶点在格 点上,建立平面直角坐标系后,点A的坐标为(-4,0),点B的坐标为(-1,0).已知Rt△ABC和Rt△A1B1C1关于y轴对称,Rt△A1B1C1和Rt△A2B2C2关于直线y=-2轴对称.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com