练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，一圆柱高8 cm，底面半径为cm，一只蚂蚁从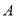点爬到点处吃食，要爬行的最短路程是（ ）cm.

    A. 6 B. 8 C. 10 D. 12

    C 【解析】【解析】 底面圆周长为2πr，底面半圆弧长为πr，即半圆弧长为： ×2π×=6（cm），展开后的图形中，有BC=8cm，AC=6cm，根据勾股定理得：AB==10（cm）．故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型：单选题

    同时抛掷A，B两个均匀的小立方体(每个面上分别标有数字1，2，3，4，5，6)，设两立方体朝上的数字分别为x，y，并以此确定点P(x，y)，那么点P落在直线y＝－2x＋9上的概率为（ ）

    A. B. C. D.

    B 【解析】试题解析：列表得： 1 2 3 4 5 6 1 （1，1） （2，1） （3，1） （4，1） （5，1） （6，1） 2 （1，2） （2，2） （3，2） （4，2） （5，2） （6，2） 3 （1，3） （2，3） （3...

    查看答案和解析>>

    科目：初中数学 来源：湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型：填空题

    不等式组的非负整数解有__________个。

    6 【解析】 由①得：x>?1， 由②得：x≤5， 不等式组的解集为：?1

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十七章达标检测卷 题型：解答题

    如图，将竖直放置的长方形砖块ABCD推倒至长方形A'B'C'D'的位置，长方形ABCD的长和宽分别为a，b，AC的长为c.

    （1）你能用只含a，b的代数式表示S△ABC，S△C'A'D'和S直角梯形A'D'BA吗?能用只含c的代数式表示S△ACA'吗?

    （2）利用(1)的结论，你能验证勾股定理吗?

    （1）S△ABC=ab，S△C'A'D'=ab，S直角梯形A'D'BA= (a+b)(a+b)= (a+b)2，S△ACA'=c2； （2）验证见解析. 【解析】试题分析：（1）易知△ABC，△C'A'D'和△ACA'都是直角三角形，根据三角形面积公式和梯形面积公式计算即可； （2）根据S△ACA'=S直角梯形A'D'BA-S△ABC-S△C'A'D，列出方程并整理即可得到结论．...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十七章达标检测卷 题型：填空题

    如果一梯子底端离建筑物9 m远，那么15 m长的梯子可达到建筑物的高度是_______m.

    12 【解析】【解析】 如图；梯子AC长是15m，梯子底端离建筑物的距离AB长为9m． 在Rt△ABC中，AC=15m，AB=9m． 根据勾股定理，得BC===12m．故答案为：12．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十七章达标检测卷 题型：单选题

    如图，已知正方形B的面积为144，正方形C的面积为169时，那么正方形A的面积为（ ）

    A. 313 B. 144 C. 169 D. 25

    D 【解析】设三个正方形的边长依次为，由于三个正方形的三边组成一个直角三角形，所以，故，即.

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型：解答题

    如图，直线y1＝2x－3与双曲线在第一象限交于点A，与x轴交于点B，过点A作AC⊥x轴，垂足为C，已知∠BAC＝∠AOC．

    （1）求A，B两点的坐标及k的值；

    （2）请直接写出当y2＞y1＞0时x的取值范围．

    （1）k=2；（2）＜x＜2 【解析】试题分析：（1）根据直线与x轴的交点，令y=0，求出点B的坐标，然后根据解直角三角形求出A点的坐标，利用待定系数法求出k的值； （2）根据函数的图像和交点，直接可写出取值范围. 试题解析：由y1＝2x－3=0，解得，所以B(，0)，OB=. 设点A的横坐标为m(m>0)，则纵坐标为2m-3,BC= ，AC=2m-3， ∵AC⊥x轴...

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型：单选题

    过⊙O内一点M的最长弦长为10cm，最短弦长为8cm，那么OM长为（ ）

    A. 3cm B. 6cm C. cm D. 9cm

    A 【解析】试题分析：由题意知，最长的弦为直径，最短的弦为垂直于直径的弦，如图所示． 直径ED⊥AB于点M， 则ED=10cm，AB=8cm， 由垂径定理知：点M为AB中点， ∴AM=4cm， ∵半径OA=5cm， ∴OM2=OA2-AM2=25-16=9， ∴OM=3cm． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：山西省吕梁市孝义市2016-2017学年九年级（上）期末考试数学试卷 题型：单选题

    如图，正五边形ABCDE内接于⊙O，过点A的切线与CB的延长线相交于点F，则∠F=（ ）

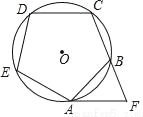
    A. 18° B. 36° C. 54° D. 72°

    D 【解析】试题分析：连接OA、OB， ∵AF是⊙O的切线， ∴∠OAF＝90°， ∵正五边形ABCDE内接于⊙O， ∴∠AOB＝＝72°， ∵OA＝OB， ∴∠OAB＝∠OBA＝＝54°， ∴∠BAF＝90°－54°＝36°， ∵∠ABF＝＝72°， ∴∠F＝180°－36°－72°＝72°， 故选D．

    查看答案和解析>>

    同步练习册答案