
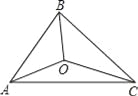
【题目】如图,△ABC的三边AB、BC、CA长分别为40、50、60.其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO= .
【答案】4:5:6.
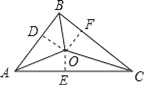
【解析】试题分析:首先过点O作OD⊥AB于点D,作OE⊥AC于点E,作OF⊥BC于点F,由OA,OB,OC是△ABC的三条角平分线,根据角平分线的性质,可得OD=OE=OF,又由△ABC的三边AB、BC、CA长分别为40、50、60,即可求得S△ABO:S△BCO:S△CAO的值. 过点O作OD⊥AB于点D,作OE⊥AC于点E,作OF⊥BC于点F,
∵OA,OB,OC是△ABC的三条角平分线, ∴OD=OE=OF,
∵△ABC的三边AB、BC、CA长分别为40、50、60,
∴S△ABO:S△BCO:S△CAO=(![]() ABOD):(
ABOD):(![]() BCOF):(
BCOF):(![]() ACOE)=AB:BC:AC=40:50:60=4:5:6.
ACOE)=AB:BC:AC=40:50:60=4:5:6.


科目:初中数学 来源: 题型:
【题目】为搞好环保,某公司准备修建一个长方体的污水处理池,池底矩形的周长为100m,则池底的最大面积是( )
A.600 m2
B.625 m2
C.650 m2
D.675 m2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2011年全年植树5亿棵,涵养水源3亿立方米.若该市以后每年平均植树5亿棵,到2017年年底“森林城市”的建设将全面完成,那时树木可以长期保持涵养水源11亿立方米.
(1)从2011年到2017年这7年时间里,该市一共要植树多少亿棵?
(2)若把2011年作为第1年,设树木涵养水源的能力y(亿立方米)与第x年成一次函数,求出该函数的表达式,并求出到第5年(即2015年)可以涵养多少水源.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列推理过程.
如图,DE∥BC,点D、A、E在同一条直线上,
求证:∠BAC+∠B+∠C=180°,
证明:∵DE∥BC
∴∠1=∠B,∠2=∠C
∵D、A、E在同一直线上(已知),
∴∠1+∠BAC+∠2=180°
∴∠BAC+∠B+∠C=180° 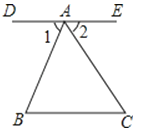
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OE平分∠AOB,且EC⊥OA,ED⊥OB,垂足分别是C,D,连结CD与OE交于点F.
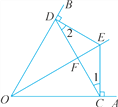
(1)求证:∠1=∠2.
(2)求证:OE是线段CD的垂直平分线.
(3)若∠1=30°,OC=2,求△OCD与△CDE的面积之差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校学生进行体育活动的情况,从全校2800名学生中随机取了100名学生,调查他们平均每天进行体育活动的时间,在这次调査中,样本是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小斌所在的7人课外活动小组在大课间活动中练习1分钟跳绳,成绩如下(单位:个):165,170,168,180,178,175,182,则这组数据的中位数是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
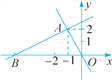
【题目】如图,一个正比例函数的图象和一个一次函数的图象交于点A(-1,2),一次函数的图象交x轴负半轴于点B,且△AOB的面积为5,求这两个函数的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com