
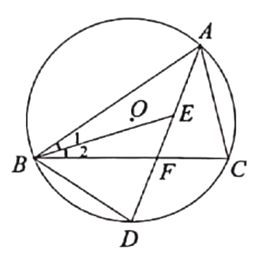
【题目】如图,△ABC内接于⊙O,∠ABC和 ∠BAC的平分线交于点E,延长AE分别交BC, ⊙O于点F, D,连接BD.
(1)求证: BD=DE.
(2)若BD=6,AD=10,求EF的长.
【答案】(1)证明见解析;(2)2.4.
【解析】
(1)根据角平分线的定义以及圆周角定理得到∠DBC=∠CAD,然后求出∠BED=∠BAD+∠1,∠DBE=∠DBC+∠2,得到∠BED=∠DBE即可;
(2)根据∠DBC=∠CAD=∠BAD,∠D=∠D,证得△DBF∽△DAB,利用相似三角形的性质列出比例式求出DF即可解决问题.
解:(1)∵AD 平分∠BAC,
∴∠BAD=∠CAD,
∴![]() =
=![]() ,
,
∴∠DBC=∠CAD,
∵BE 平分∠ABC,
∴∠1=∠2,
∵∠BED=∠BAD+∠1,∠DBE=∠DBC+∠2,
∴∠BED=∠DBE,
∴DB=DE;
(2)由(1)得∠DBC=∠CAD=∠BAD,
∵∠D=∠D,
∴△DBF∽△DAB,
∴![]() ,
,
∵BD=6,AD=10,
∴![]() ,
,
∴DF=3.6,
∵DE=BD=6,
∴EF=DE-DF=6-3.6=2.4.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某超市销售一种饮料, 每瓶进价为![]() 元,当每瓶售价
元,当每瓶售价![]() 元时,日均销售量
元时,日均销售量![]() 瓶.经市场调查表明,每瓶售价每增加
瓶.经市场调查表明,每瓶售价每增加![]() 元,日均销售量减少
元,日均销售量减少![]() 瓶.
瓶.
(1)当每瓶售价为![]() 元时,日均销售量为 瓶;
元时,日均销售量为 瓶;
(2)当每瓶售价为多少元时,所得日均总利润为![]() 元;
元;
(3)当每瓶售价为多少元时,所得日均总利润最大?最大日均总利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超越公司将某品牌农副产品运往新时代市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从超越公司出发,能否在上午10:00之前到达新时代市场?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程mx2-2mx+m-2=0.
(1)若方程有两个不等实数根,求m的取值范围;
(2)若方程的两实数根为x1,x2,且|x1-x2|=1,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
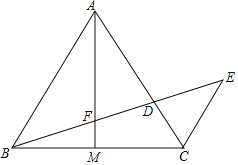
【题目】如图,△ABC中,AB=AC,AM为BC边的中线,点D在边AC上,联结BD交AM于点F,延长BD至点E,使得![]() =
=![]() ,联结CE.
,联结CE.
求证:(1)∠ECD=2∠BAM;
(2)BF是DF和EF的比例中项.
查看答案和解析>>
科目:初中数学 来源: 题型:
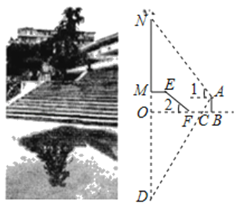
【题目】如图,雨后初睛,李老师在公园散步,看见积水水面上出现阶梯上方树的倒影,于是想利用倒影与物体的对称性测量这颗树的高度,他的方法是:测得树顶的仰角∠1、测量点A到水面平台的垂直高度AB、看到倒影顶端的视线与水面交点C到AB的水平距离BC.再测得梯步斜坡的坡角∠2和长度EF,根据以下数据进行计算,如图,AB=2米,BC=1米,EF=4![]() 米,∠1=60°,∠2=45°.已知线段ON和线段OD关于直线OB对称.(以下结果保留根号)
米,∠1=60°,∠2=45°.已知线段ON和线段OD关于直线OB对称.(以下结果保留根号)
(1)求梯步的高度MO;
(2)求树高MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高教学质量,促进学生全面发展,某中学计划投入99000元购进一批多媒体设备和电脑显示屏,且准备购进电脑显示屏的数量是多媒体设备数量的6倍. 现从商家了解到,一套多媒体设备和一个电脑显示屏的售价分别为3000元和600元.
(1)求最多能购进多媒体设备多少套?
(2)恰逢“双十一”活动,每套多媒体设备的售价下降![]() ,每个电脑显示屏的售价下降
,每个电脑显示屏的售价下降![]() 元,学校决定多媒体设备和电脑显示屏的数量在(1)中购进最多量的基础上都增加
元,学校决定多媒体设备和电脑显示屏的数量在(1)中购进最多量的基础上都增加![]() ,实际投入资金与计划投入资金相同,求
,实际投入资金与计划投入资金相同,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com