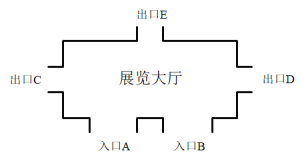
[题目]如图.某科技物展览大厅有A.B两个入口.C.D.E三个出口.小昀任选一个入口进入展览大厅. 参观结束后任选一个出口离开.(1)若小昀已进入展览大厅.求他选择从出口C离开的概率.(2)求小昀选择从入口A进入.从出口E离开的概率.(请用列表或画树状图求解) 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，某科技物展览大厅有A、B两个入口，C、D、E三个出口.小昀任选一个入口进入展览大厅，参观结束后任选一个出口离开.

(1)若小昀已进入展览大厅，求他选择从出口C离开的概率.

(2)求小昀选择从入口A进入，从出口E离开的概率.(请用列表或画树状图求解)

【答案】(1); (2)

【解析】

（1）用列举法即可求得；

（2）画树状图（见解析）得出所有可能的结果，再分析求解即可.

（1）小昀选择出口离开时的所有可能有3种：C、D、E，每一种可能出现的可能性都相等，因此他选择从出口C离开的概率为：；

（2）根据题意画树状图如下：

由树状图可以看出，所有可能出现的结果共有6种，即（AC）、（AD）、（AE）、（BC）、（BD）、（BE），这些结果出现的可能性相等

所以小昀选择从入口A进入，出口E离开（即AE）的概率为.

练习册系列答案

智慧课堂密卷100分单元过关检测系列答案

超效单元测试AB卷系列答案

单元期中期末卷系列答案

夺冠小状元课时作业本系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如果一元二次方程ax2+bx+c＝0 的两根 x1，x2均为正数，其中x1＞x2，且满足1＜x1﹣x2＜2，那么称这个方程有“友好根”．

（1）方程（x﹣）（x﹣）＝0_____“友好根”（填：“有”或“没有”）；

（2）已知关于x的 x2﹣（t﹣1）x+t﹣2＝0有“友好根”，求 t的取值范围．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，AB为⊙O的直径，C是⊙O上一点，过点C的直线交AB的延长线于点D，AE⊥DC，垂足为E，F是AE与⊙O的交点，AC平分∠BAE．

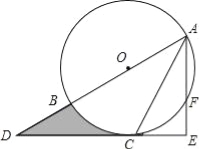
（1）求证：DE是⊙O的切线；

（2）若AE=6，∠D=30°，求图中阴影部分的面积．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】综合与探究

如图，在平面直角坐标系中，已知抛物线与x轴交于A，B两点，与y轴交于点C，直线l经过坐标原点O，与抛物线的一个交点为D，与抛物线的对称轴交于点E，连接CE，已知点A，D的坐标分别为（－2，0），（6，－8）．

（1）求抛物线的函数表达式，并分别求出点B和点E的坐标；

（2）试探究抛物线上是否存在点F，使≌，若存在，请直接写出点F的坐标；若不存在，请说明理由；

（3）若点P是y轴负半轴上的一个动点，设其坐标为（0，m），直线PB与直线l交于点Q．试探究：当m为何值时，是等腰三角形．

查看答案和解析>>

科目：初中数学 来源： 题型：

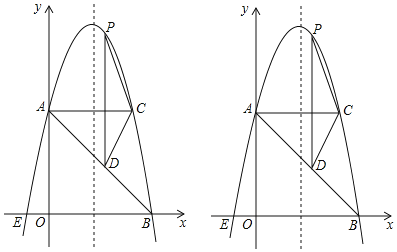
【题目】如图，在平面直角坐标系中，抛物线y＝ax2+bx+c的顶点坐标为(2，9)，与y轴交于点A(0，5)，与x轴交于点E，B．

（1）求二次函数y＝ax2+bx+c的解析式；

（2）过点A作AC平行于x轴，交抛物线于点C，点P为抛物线上的一点（点P在AC上方），作PD平行于y轴交AB于点D，问当点P在何位置时，线段PD最长？并求出最大值；

（3）若点M在抛物线上，点N在其对称轴上，使得以A，E，N，M为顶点的四边形是平行四边形，求点M的坐标．（请直接写出结果）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在平面直角坐标系中，已知点A（―3，6）、B（―9，一3），以原点O为位似中心，相似比为，把△ABO缩小，则点A的对应点A′的坐标是（）

A．（―1，2）

B．（―9，18）

C．（―9，18）或（9，―18）

D．（―1，2）或（1，―2）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图所示，已知二次函数y＝ax2+bx+c的图象与x轴交于A，B两点，与y轴交于点C，对称轴为直线x＝1．直线y＝﹣x+c与抛物线y＝ax2+bx+c交于C，D两点，D点在x轴下方且横坐标小于3，则下列结论：①a﹣b+c＜0；②2a+b+c＞0；③x（αx+b）≤a+b；④a＞﹣1．其中正确的有（　　）