
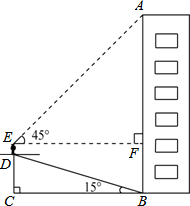
 小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.(以下计算结果精确到0.1m)
小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.(以下计算结果精确到0.1m)分析 (1)利用在Rt△BCD中,∠CBD=15°,BD=20,得出CD=BD•sin15°求得答案即可;
(2)由图可知:AB=AF+DE+CD,利用直角三角形的性质和锐角三角函数的意义求得AF得出答案即可.
解答 解:(1)在Rt△BCD中,∠CBD=15°,BD=20,
∴CD=BD•sin15°,
∴CD≈5.2(m).
答:小华与地面的垂直距离CD的值是5.2m;
(2)在Rt△AFE中,
∵∠AEF=45°,
∴AF=EF=BC,
由(1)知,BC=BD•cos15°≈19.3(m),
∴AB=AF+DE+CD=19.3+1.6+5.2=26.1(m).
答:楼房AB的高度是26.1m.
点评 本题考查了解直角三角形的应用,题目中涉及到了仰俯角和坡度角的问题,解题的关键是构造直角三角形.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:选择题
| A. | 1500条 | B. | 1600条 | C. | 1700条 | D. | 3000条 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上,此时,光盘与AB,CD分别相切于点N,M.现从如图所示的位置开始,将光盘在直尺边上沿着CD向右滚动到再次与AB相切时,光盘的圆心经过的距离是$\frac{4\sqrt{3}}{3}$.
小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上,此时,光盘与AB,CD分别相切于点N,M.现从如图所示的位置开始,将光盘在直尺边上沿着CD向右滚动到再次与AB相切时,光盘的圆心经过的距离是$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.
如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{45}{2}$ | B. | $\frac{49}{2}$ | C. | $\frac{45}{2}$或2 | D. | $\frac{49}{2}$或2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com