
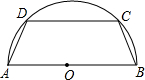
 (2007•安溪县质检)如图,有一块半径为5cm的半圆形钢板,计划截成等腰梯形ABCD的形状,他的下底AB是⊙O的直径,上底CD的端点在圆周上.
(2007•安溪县质检)如图,有一块半径为5cm的半圆形钢板,计划截成等腰梯形ABCD的形状,他的下底AB是⊙O的直径,上底CD的端点在圆周上.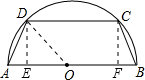 (1)过点D作DE⊥AB,CF⊥AB,连接OD,
(1)过点D作DE⊥AB,CF⊥AB,连接OD,| 5 2-4 2 |
| AD |
| AB |
| AE |
| AD |
| AD2 |
| AB |
| x 2 |
| 10 |
| x 2 |
| 10 |
| x 2 |
| 5 |
| x 2 |
| 5 |
| 1 |
| 5 |
| x 2 |
| 5 |
| x 2 |
| 5 |
| 2 |
| 1 |
| 5 |
| 1 |
| 5 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
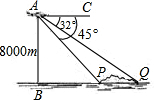 (2007•安溪县质检)一架飞机在海拔8000m的高度飞行,在空中测出前下方海岛两侧海岸俯角分别是32°和45°,计算这个海岛的宽度PQ.(精确到1m)
(2007•安溪县质检)一架飞机在海拔8000m的高度飞行,在空中测出前下方海岛两侧海岸俯角分别是32°和45°,计算这个海岛的宽度PQ.(精确到1m)查看答案和解析>>
科目:初中数学 来源: 题型:
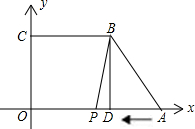 ,经O点再往OC方向移动,最后到达C点.设点P移动时间为t秒.
,经O点再往OC方向移动,最后到达C点.设点P移动时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com