
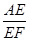 =3,求
=3,求 的值.
的值.
 的值是________.
的值是________.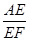 =m(m>0)则
=m(m>0)则 的值是________(用含有m的代数式表示),试写出解答过程.
的值是________(用含有m的代数式表示),试写出解答过程. =a,
=a, =b(a>0,b>0)则
=b(a>0,b>0)则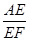 的值是________(用含a、b的代数式表示).
的值是________(用含a、b的代数式表示).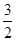 (2)
(2)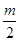 (3)ab+1
(3)ab+1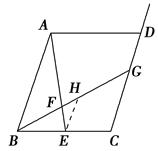
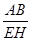 =
=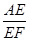 =3,
=3, =
= =
=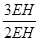 =
=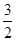
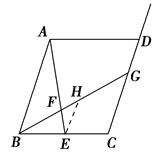
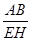 =
=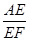 =m,
=m,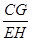 =
= =2,∴CG=2EH,∴
=2,∴CG=2EH,∴ =
= =
=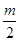

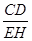 =
= =b,
=b, =a,
=a,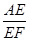 =
=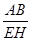 =
=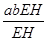 =ab
=ab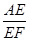 =
= =
=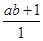 =ab+1
=ab+1

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:解答题
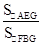 的值.
的值.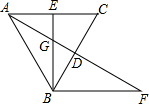
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
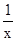 图象上的一个动点,过点P作PQ⊥x轴,垂足为Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有( )
图象上的一个动点,过点P作PQ⊥x轴,垂足为Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有( )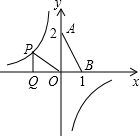
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
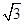 ,将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
,将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.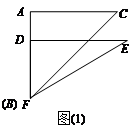
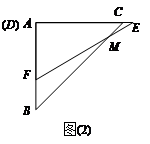
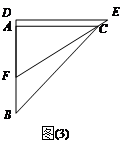
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
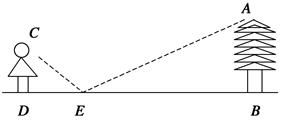
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
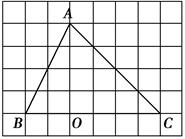
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
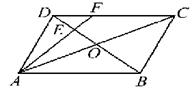
| A.1∶4 | B.1∶3 | C.2∶3 | D.1∶2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com