
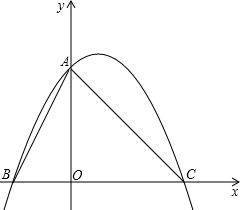
将直角边长为6的等腰Rt△AOC放在如图所示的平面直角坐标系中,点O为坐标原点,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(–3,0).
(1)求该抛物线的解析式;
(2)若点P是线段BC上一动点,过点P作AB的平行线交AC于点E,连接AP,当△APE的面积最大时,求点P的坐标;
(3)在第一象限内的该抛物线上是否存在点G,使△AGC的面积与(2)中△APE的最大面积相等?若存在,请求出点G的坐标;若不存在,请说明理由.
|
解:(1)如图,∵抛物线y=ax2+bx+c(a ≠ 0)的图象经过点A(0,6),
∴c=6. 1分 ∵抛物线的图象又经过点(–3,0)和(6,0), ∴ 解之,得 故此抛物线的解析式为:y=- (2)设点P的坐标为(m,0), 则PC=6-m,S△ABC= ∵PE∥AB, ∴△CEP∽△CAB 6分 ∴ ∴S△CEP= ∵S△APC= ∴S△APE=S△APC-S△CEP=3(6-m)- 当m= (3)如图,过G作GH⊥BC于点H,设点G的坐标为G(a,b),9分
连接AG、GC, ∵S梯形AOHG= S△CHG= ∴S四边形AOCG= ∵S△AGC=S四边形AOCG-S△AOC ∴ ∵点G(a,b)在抛物线y=- ∴b=- ∴ 化简,得4a2-24a+27=0 解之,得a1= 故点G的坐标为( |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
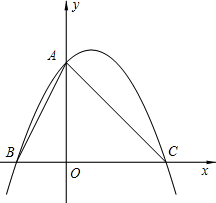 ,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(-3,0).
,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(-3,0).查看答案和解析>>
科目:初中数学 来源: 题型:
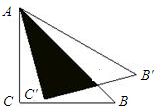 将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后,得到△AB′C′,则图中阴影部分的面积是( )cm2.
将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后,得到△AB′C′,则图中阴影部分的面积是( )cm2.| A、12.5 | ||||
B、
| ||||
C、
| ||||
| D、不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com