
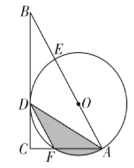
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的平分线,经过
的平分线,经过![]() 两点的圆的圆心
两点的圆的圆心![]() 恰好落在
恰好落在![]() 上,
上,![]() 分别与
分别与![]() 交于点
交于点![]() .若
.若![]() .则图中阴影部分的面积为( )
.则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
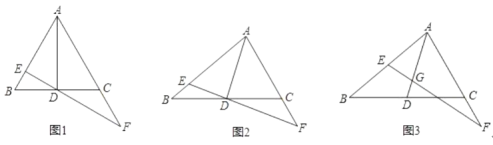
【题目】![]() 中,
中,![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上(点
上(点![]() 不与
不与![]() 重合),过点
重合),过点![]() 的直线交
的直线交![]() 于
于![]() ,交射线
,交射线![]() 于点
于点![]() ,设
,设![]() ,
,![]() .
.
(1)如图1,若![]() 为等边三角形,点
为等边三角形,点![]() 与
与![]() 重合,
重合,![]() ,求证:
,求证:![]() ;
;
(2)如图2,若点![]() 与
与![]() 重合,求证:
重合,求证:![]() ;
;
(3)如图3,若![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两家草莓采摘园,草莓的销售价格相间,在生长旺季,两家均排出优惠方案.甲园的优惠方案是:采摘的草莓不超过![]() 时,按原价销售;若超过
时,按原价销售;若超过![]() 超过部分
超过部分![]() 折优惠;乙园的优惠方案是:游客进园需购买
折优惠;乙园的优惠方案是:游客进园需购买![]() 元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓
元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓![]() 时,所需费用相同.
时,所需费用相同.
在乙采摘园所需费用![]() ( 元)与草梅采摘量
( 元)与草梅采摘量![]() (千克)满足一次函数关系,如下表:
(千克)满足一次函数关系,如下表:
数量 |
|
|
|
| ··· |
费用 |
|
|
|
| ··· |
(1)求![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的范围);
的范围);
(2)求两个采摘园的草莓在生长旺季前的销售价格.并求在甲采摘园所需费用![]() (元)与草莓采摘量
(元)与草莓采摘量![]() (千克)的函数关系式
(千克)的函数关系式![]() ;
;
(3)若嘉琪准备花费![]() 元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
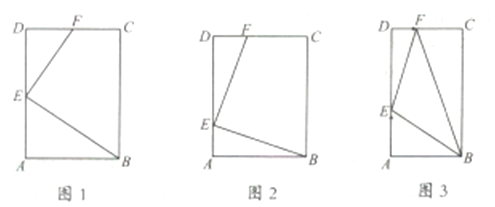
【题目】矩形![]() 中,
中,![]() (其中
(其中![]() )
)
(1)点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() ;
;
①如图![]() ,若
,若![]() ,且点
,且点![]() 是
是![]() 中点,求证
中点,求证![]() ;
;
②如图![]() ,若
,若![]() ,且
,且![]() ,求证:
,求证:![]() ;
;
(2)如图![]() ,当
,当![]() ,
,![]() 时,点
时,点![]() 以
以![]() 的速度从
的速度从![]() 到
到![]() ,点
,点![]() 以
以![]() 的速度从
的速度从![]() 到
到![]() ,当点
,当点![]() 到
到![]() 时两点都停止运动,则点
时两点都停止运动,则点![]() 的运动时间
的运动时间![]() 为多少时,
为多少时,![]() 的面积
的面积![]() 最小,最小面积为多少?
最小,最小面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有6张卡片,6张卡片的正面分别标有数字﹣4,﹣3,﹣2,﹣1,6,8,这些卡片除数字外都相同,将卡片搅匀.
(1)从盒子中任意抽取一张卡片,求恰好抽到标有偶数卡片的概率;
(2)先从盒子中任意抽取一张卡片,把它上面的数字作为一个点的横坐标,不放回,再从盒子剩余的卡片中任意抽取一张卡片,把它上面的数字作为这个点的纵坐标,求抽取的点恰好落在第二象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成相应任务:
黄金分割
天文学家开普勒把黄金分割称为神圣分割,并指出毕达哥拉斯定理(勾股定理)和黄金分割是几何中的双宝,前者好比黄金,后者堪称珠宝,历史上最早正式在书中使用“黄金分割”这个名称的是欧姆,19世纪以后“黄金分割”的说法逐渐流行起来,黄金分割被广泛应用于建筑等领域.黄金分割指把一条线段分为两部分,使其中较长部分与线段总长之比等于较短部分与较长部分之比,该比值为![]() .用下面的方法(如图①)就可以作出已知线段
.用下面的方法(如图①)就可以作出已知线段![]() 的黄金分割点
的黄金分割点![]() :
:

①以线段![]() 为边作正方形
为边作正方形![]() ,
,
②取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
③延长![]() 到
到![]() ,使
,使![]() ,
,
④以线段![]() 为边作正方形
为边作正方形![]() ,点
,点![]() 就是线段
就是线段![]() 的黄金分割点.
的黄金分割点.
以下是证明点![]() 就是线段
就是线段![]() 的黄金分割点的部分过程:
的黄金分割点的部分过程:
证明:设正方形![]() 的边长为1,则
的边长为1,则![]() ,
,
![]() 为
为![]() 中点,
中点,
![]() ,
,
![]() 在
在![]() 中,
中,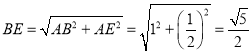 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
…
任务:
(1)补全题中的证明过程;
(2)如图②,点![]() 为线段
为线段![]() 的黄金分割点,分别以
的黄金分割点,分别以![]() 为边在线段
为边在线段![]() 同侧作正方形
同侧作正方形![]() 和矩形
和矩形![]() ,连接
,连接![]() .求证:
.求证:![]() ;
;
(3)如图③,在正五边形![]() 中,对角线
中,对角线![]() 与
与![]() 分别交于点
分别交于点![]() 求证:点
求证:点![]() 是
是![]() 的黄金分割点.
的黄金分割点.
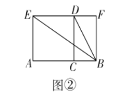
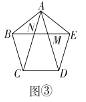
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:小明为了计算![]() 的值 ,采用以下方法:
的值 ,采用以下方法:
设![]() ①
①
则![]() ②
②
②-①得 ![]()
∴![]()
(1)![]() = ;
= ;
(2)![]() = ;
= ;
(3)求![]() 的和(
的和(![]() ,
,![]() 是正整数,请写出计算过程 ).
是正整数,请写出计算过程 ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两家草莓采摘园,草莓的销售价格相间,在生长旺季,两家均排出优惠方案.甲园的优惠方案是:采摘的草莓不超过![]() 时,按原价销售;若超过
时,按原价销售;若超过![]() 超过部分
超过部分![]() 折优惠;乙园的优惠方案是:游客进园需购买
折优惠;乙园的优惠方案是:游客进园需购买![]() 元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓
元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓![]() 时,所需费用相同.
时,所需费用相同.
在乙采摘园所需费用![]() ( 元)与草梅采摘量
( 元)与草梅采摘量![]() (千克)满足一次函数关系,如下表:
(千克)满足一次函数关系,如下表:
数量 |
|
|
|
| ··· |
费用 |
|
|
|
| ··· |
(1)求![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的范围);
的范围);
(2)求两个采摘园的草莓在生长旺季前的销售价格.并求在甲采摘园所需费用![]() (元)与草莓采摘量
(元)与草莓采摘量![]() (千克)的函数关系式
(千克)的函数关系式![]() ;
;
(3)若嘉琪准备花费![]() 元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,创新小组要测量公园内一棵树的高度AB,其中一名小组成员站在距离树10米的点E处,测得树顶A的仰角为54°.已知测角仪的架高CE=1.8米,则这颗树的高度为_________米.(结果保留一位小数.参考数据:sin54°=0.8090,cos54°=0.5878,tan54°=1.3764)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com