
【题目】如右图,在△ABC中,点Q,P分别是边AC,BC上的点,AQ=PQ,PR⊥AB于R,PS⊥AC于S,且PR=PS,下面四个结论:①AP平分∠BAC;②AS=AR;③BP=QP;④QP∥AB.其中一定正确的是( )
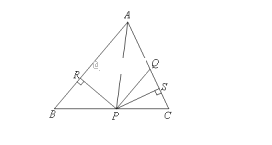
A. ①②③ B. ①③④ C. ①②④ D. ②③④
科目:初中数学 来源: 题型:
【题目】在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.在建立平面直角坐标系后,点B的坐标为(﹣1,2).
(1)把△ABC向下平移8个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出与△A1B1C1关于y轴对称的△A2B2C2;
(3)若点P(a,b)是△ABC边上任意一点,P2是△A2B2C2边上与P对应的点,写出P2的坐标为 ;
(4)试在y轴上找一点Q(在图中标出来),使得点Q到B2、C2两点的距离之和最小,并求出QB2+QC2的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若△ABC≌△MNP,∠A=∠M,∠C=∠P,AB=4cm,BC=2cm,则 NP=( )
A. 2cm B. 3cm C. 4cm D. 6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=(m﹣2)x+2与正比例函数y2=2x图象相交于点A(2,n),一次函数y1=(m﹣2)x+2与x轴交于点B.
(1)求m、n的值;
(2)求△ABO的面积;
(3)观察图象,直接写出当x满足 时,y1>y2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:
(1)画出△ABC关于y轴的对称图形△A1B1C1;
(2)请计算△ABC的面积;
(3)直接写出△ABC关于x轴对称的三角形△A2B2C2的各点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
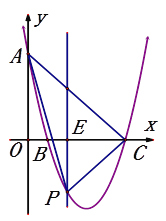
【题目】在平面直角坐标系中,抛物线![]() 与y轴的交点为A,与x轴的正半轴分别交于点B(b,0),C(c,0).
与y轴的交点为A,与x轴的正半轴分别交于点B(b,0),C(c,0).
(1)当b=1时,求抛物线相应的函数表达式;
(2)当b=1时,如图,E(t,0)是线段BC上的一动点,过点E作平行于y轴的直线l与抛物线的交点为P.求△APC面积的最大值;
(3)当c =b+ n.时,且n为正整数.线段BC(包括端点)上有且只有五个点的横坐标是整数,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中放入一个矩形纸片ABCO,将纸片翻折后,点B恰好落在![]() 轴上,记为
轴上,记为![]() ,折痕为CE.直线CE的关系式是
,折痕为CE.直线CE的关系式是![]() ,与
,与![]() 轴相交于点F,且AE=3.
轴相交于点F,且AE=3.
(1)求OC长度;
(2)求点![]() 的坐标;
的坐标;
(3)求矩形ABCO的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com