
����Ŀ����ͼ����ABC�ǵȱ������Σ���D��BC����һ���㣬��E��F�ֱ���AB��AC���ϣ�����AD��DE��DF���ҡ�ADE=��ADF=60�㣮
С��ͨ���۲졢ʵ�飬������룺�ڵ�D�˶��Ĺ����У�ʼ����AE=AF��С�������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ���֤���ò���ļ����뷨��
�뷨1������AD�ǡ�EDF�Ľ�ƽ���ߣ������ADF��ȫ�������Σ�Ȼ��ͨ�����������ε����֪ʶ��֤��
�뷨2������AD�ǡ�EDF�Ľ�ƽ���ߣ������ƽ���ߵ����ʶ����Ļ���ͼ�Σ�Ȼ��ͨ��ȫ�������ε����֪ʶ��֤��
�뷨3������ACD�Ƶ�A˳ʱ����ת����ABG��ʹ��AC��AB�غϣ�Ȼ��ͨ��ȫ�������ε����֪ʶ��֤��
����ο�������뷨������С��֤��AE=AF����һ�ַ������ɣ�

���𰸡�������
��������
�뷨1����DE�Ͻ�ȡDG=DF������AG�����ж���ADG�ա�ADF���õ�AG=AF���ٸ��ݡ�AEG=��AGE���ó�AE=AG�������õ�AE=AF��
�뷨2����A��AG��DE��G��AH��DF��H�����ݽ�ƽ���ߵ����ʵõ�AG=AH�������ж���AEG�ա�AFH�����ɵõ�AE=AF��
�뷨3������ACD���ŵ�A˳ʱ����ת����ABG��ʹ��AC��AB�غϣ�����DG���ж���AGD�ǵȱ������Σ������ó���AGE�ա�ADF�����ɵõ�AE=AF��
֤����
�뷨1����ͼ����DE�Ͻ�ȡDG=DF������AG��
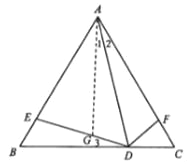
�ߡ�ABC�ǵȱ������Σ�
���B=��C=60�㣬
�ߡ�ADE=��ADF=60�㣬AD=AD��
���ADG�ա�ADF��
��AG=AF����1=��2��
�ߡ�ADB=60��+��3=60��+��2��
���3=��2��
���3=��1��
�ߡ�AEG=60��+��3����AGE=60��+��1��
���AEG=��AGE��
��AE=AG��
��AE=AF��
�뷨2����ͼ����A��AG��DE��G��AH��DF��H��
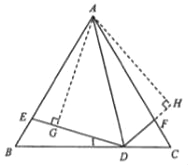
�ߡ�ADE=��ADF=60�㣬
��AG=AH��
�ߡ�FDC=60�㩁��1��
���AFH=��DFC=60��+��1��
�ߡ�AED=60��+��1��
���AEG=��AFH��
���AEG�ա�AFH��
��AE=AF��
�뷨3����ͼ������ACD���ŵ�A˳ʱ����ת����ABG��ʹ��AC��AB�غϣ�����DG��

���ABG�ա�ACD��
��AG=AD����GAB=��DAC��
�ߡ�ABC�ǵȱ������Σ�
���BAC=��ABC=��C=60�㣬
���GAD=60�㣬
���AGD�ǵȱ������Σ�
���ADG=��AGD=60�㣬
�ߡ�ADE=60�㣬
��G��E��D���㹲�ߣ�
���AGE�ա�ADF��
��AE=AF��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʦ�˶����У��ף��������ʦ�μӡ����˱����������ܱ���������ÿ��������ʦ�ñ�������������涨��·�̣���;�������ʱ����ص����������ܣ���ʱ����ʤ���������ľ�����y���ף���ʾ��ʱ����x���룩��ʾ����ͼ��ʾ�����ʦ����������y��x�ĺ�����ϵ��ͼ����ͼ���������ĸ��ƶϣ�
�������ʦ��ʤ
�������ʦ������ʱ���2��
�ۼ����ʦȥʱ�ٶ�Ϊ0.5��/��
�ܷ���ʱ�����ʦ�������ʦ���ٶȱ���2:3
���к������ǣ� ��
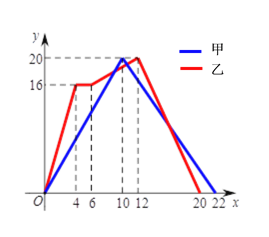
A. �٢� B. �٢� C. �ڢ� D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� 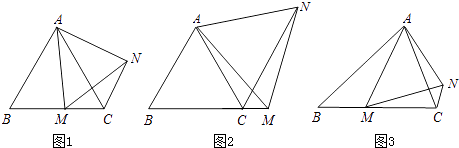
��1����������⡿
��ͼ1���ڵȱߡ�ABC�У���M��BC�ϵ�����һ�㣨�����˵�B��C��������AM����AMΪ�����ȱߡ�AMN������CN����֤����ABC=��ACN��
��2�������̽����
��ͼ2���ڵȱߡ�ABC�У���M��BC�ӳ����ϵ�����һ�㣨�����˵�C���������������䣬��1���н��ۡ�ABC=��ACN����������˵�����ɣ�
��3������չ���졿
��ͼ3���ڵ�����ABC�У�BA=BC����M��BC�ϵ�����һ�㣨�����˵�B��C��������AM����AMΪ����������AMN��ʹ���ǡ�AMN=��ABC������CN����̽����ABC���ACN��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�����ǰ�Ͱ�Բ����������ͼ�з�ʽ���ţ����ǰ�һ��������������̶�������ֱ���غϣ��ص����ֵ����������� ![]() ����Ӧ��Բ�Ľǣ���AOB��Ϊ120�㣬OC�ij�Ϊ2cm�������ǰ���������ص����ֵ����Ϊ ��
����Ӧ��Բ�Ľǣ���AOB��Ϊ120�㣬OC�ij�Ϊ2cm�������ǰ���������ص����ֵ����Ϊ �� 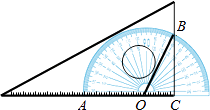
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ֹ��������ϣ���ʦ��֯���꼶��2�����ѧ����Ӳֽ����Բ���β�ҶͲ�����꼶��2�����ѧ��44�ˣ���������������Ů��������2�ˣ�����ÿ��ѧ��ÿСʱ��Ͳ��50�����Ͳ��120����
��1�����꼶��2������������Ů���������ˣ�
��2��Ҫ��һ��Ͳ��������Ͳ�ף�Ϊ��ʹÿСʱ������Ͳ����Ͳ�պ����ף�Ӧ�÷��������ѧ����Ͳ����������ѧ����Ͳ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2013��5��7���㽭ʡ11�����еĿ�������ָ����AQI����ͼ��ʾ�� 
��1����11�����е���Ŀ�������ָ���ļ����������λ���ֱ��Ƕ��٣�
��2����0��AQI��50ʱ����������Ϊ�ţ�����11�����е���Ŀ�������Ϊ�ŵ�Ƶ�ʣ�
��3�������������ˡ���ɽ�����ˡ�̨��������е���Ŀ�������ָ����ƽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��A�������ϱ�ʾ+2�ĵ㿪ʼ�ƶ�����һ���������ƶ�1����λ���������ƶ�2����λ���ڶ����������ƶ�3����λ���������ƶ�4����λ���������������ƶ�5����λ���������ƶ�6����λ����
��1��д����һ���ƶ���������������ϱ�ʾ����Ϊ ��
��2��д���ڶ����ƶ���������������ϱ�ʾ����Ϊ ��
��3��д��������ƶ���������������ϱ�ʾ����Ϊ ��
��4��д����![]() ���ƶ����������������ϱ�ʾ����Ϊ ��
���ƶ����������������ϱ�ʾ����Ϊ ��
��5�������![]() ���ƶ���������������ϱ�ʾ����Ϊ56����
���ƶ���������������ϱ�ʾ����Ϊ56����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y= ![]() x2+bx��ֱ��y=2x���ڵ�O��0��0����A��a��12������B����������O��A֮���һ�����㣬����B�ֱ���x�ᡢy���ƽ������ֱ��OA���ڵ�C��E��
x2+bx��ֱ��y=2x���ڵ�O��0��0����A��a��12������B����������O��A֮���һ�����㣬����B�ֱ���x�ᡢy���ƽ������ֱ��OA���ڵ�C��E��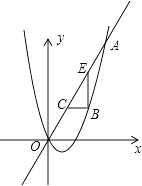
��1���������ߵĺ�������ʽ��
��2������CΪOA���е㣬��BC�ij���
��3����BC��BEΪ�߹������BCDE�����D������Ϊ��m��n�������m��n֮��Ĺ�ϵʽ��
��4��������OA��ԭ����ת45�㲢�������߽��ڵ�P�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y= ![]() ��x��m��2��
��x��m��2�� ![]() m2+m�Ķ���ΪA����y��Ľ���ΪB������AB��AC��AB����y���ڵ�C���ӳ�CA����D��ʹAD=AC������BD����AE��x�ᣬDE��y�ᣮ
m2+m�Ķ���ΪA����y��Ľ���ΪB������AB��AC��AB����y���ڵ�C���ӳ�CA����D��ʹAD=AC������BD����AE��x�ᣬDE��y�ᣮ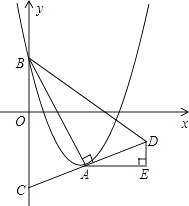
��1����m=2ʱ�����B�����ꣻ
��2����DE�ij���
��3�������D������Ϊ��x��y������y����x�ĺ�����ϵʽ���ڹ���D��AB��ƽ���ߣ���ڣ�3������ȷ���ĺ���ͼ�����һ������ΪP����mΪ��ֵʱ����A��B��D��PΪ������ı�����ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com