
��ͼ��ʾ������״�ʹ�С��ȷ���ġ�ABC�У�BC=6��E��F�ֱ���AB��AC���е㣬P��EF��EF���ӳ����ϣ�BP��CE��D��Q��CE����BQƽ�֡�CBP����BP=y��PE=x��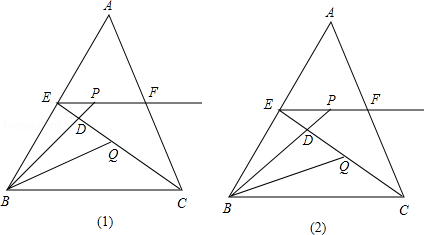
��1����x= EFʱ����S��DPE��S��DBC��ֵ��
EFʱ����S��DPE��S��DBC��ֵ��
��2����CQ= CEʱ����y��x֮��ĺ�����ϵʽ��
CEʱ����y��x֮��ĺ�����ϵʽ��
��3���ٵ�CQ= CEʱ����y��x֮��ĺ�����ϵʽ��
CEʱ����y��x֮��ĺ�����ϵʽ��
�ڵ�CQ= CE��nΪ��С��2�ij�����ʱ��ֱ��д��y��x֮��ĺ�����ϵʽ��
CE��nΪ��С��2�ij�����ʱ��ֱ��д��y��x֮��ĺ�����ϵʽ��
�⣺��1����E��F�ֱ���AB��AC���е㣬x= EF��
EF��
��EF��BC����EF= BC��
BC��
���EDP�ס�CDB��
��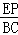 =
= ��
��
��S��DPE��S��DBC=1��36��
��2������ͼ����CQ=a��DE=b��BD=c����DP=y��c��
������EQ=kCQ=ka��k��0������DQ=ka��b��CD=��k+1��a��b��
��Q����QM��BC�ڵ�M����QN��BP�ڵ�N��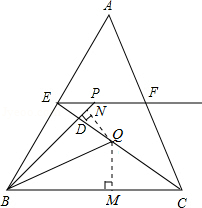
��BQƽ�֡�CBP����QM=QN��
��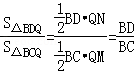 ��
��
�֡�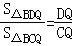 ��
��
��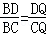 ����
����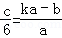 ��
��
��EP��BC����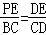 ����
����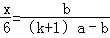 ��
��
��EP��BC����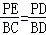 ����
����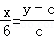 ��
��
�ɢ٢ڢ�ʽ������ã�y=6k��x ��
��CQ= CEʱ��k=1����y��x֮��ĺ�����ϵʽΪ��y=6��x��
CEʱ��k=1����y��x֮��ĺ�����ϵʽΪ��y=6��x��
��3����CQ= CEʱ��k=2���ɣ�2���Т�ʽ��֪��y��x֮��ĺ�����ϵʽΪ��y=12��x��
CEʱ��k=2���ɣ�2���Т�ʽ��֪��y��x֮��ĺ�����ϵʽΪ��y=12��x��
��CQ= CE��nΪ��С��2�ij�����ʱ��k=n��1���ɣ�2���Т�ʽ��֪��y��x֮��ĺ�����ϵʽΪ��y=6��n��1����x��
CE��nΪ��С��2�ij�����ʱ��k=n��1���ɣ�2���Т�ʽ��֪��y��x֮��ĺ�����ϵʽΪ��y=6��n��1����x��
����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ÿ���12��1�������簬�̲������գ���һ�����簬�̲�����ϣ����̲�������Ⱦ�ߺͰ��̲����������������ǵ����⣬һ�������ĺ�˿�����ȿ���������᳡�Ͽգ�֧�����ǽ���˿������С�Σ��ñ��뽫�۵��õĺ�˿��������ǰ����˿���Ӵ˳�Ϊ���̲����ε���������ͼ��ʾ�����˿�����ص����ֵ���״��
ÿ���12��1�������簬�̲������գ���һ�����簬�̲�����ϣ����̲�������Ⱦ�ߺͰ��̲����������������ǵ����⣬һ�������ĺ�˿�����ȿ���������᳡�Ͽգ�֧�����ǽ���˿������С�Σ��ñ��뽫�۵��õĺ�˿��������ǰ����˿���Ӵ˳�Ϊ���̲����ε���������ͼ��ʾ�����˿�����ص����ֵ���״���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ij�����죬С�������İְֿ���һ���������ϵĴ��״ε�ij�ų����ۣ����������²ŷ��ֹų���Ϊ��������״����ͼ��ʾ����С���İְְѳ�ͣ�ڳ����⣬��ϸ������ŵĸߺͿ��Լ��Լ������Ĵ�С��ʮ�ֵ��Ŀ����Ƿ��ܹ�˳��ͨ������ѯ�ʵ�֪�����ŵײ��Ŀ�Ϊ6�ף���ߵ�������5�ף���������ĸ���4�ף���������2.8�ף���ô�����ܷ�˳��ͨ����˵�����ɣ���
ij�����죬С�������İְֿ���һ���������ϵĴ��״ε�ij�ų����ۣ����������²ŷ��ֹų���Ϊ��������״����ͼ��ʾ����С���İְְѳ�ͣ�ڳ����⣬��ϸ������ŵĸߺͿ��Լ��Լ������Ĵ�С��ʮ�ֵ��Ŀ����Ƿ��ܹ�˳��ͨ������ѯ�ʵ�֪�����ŵײ��Ŀ�Ϊ6�ף���ߵ�������5�ף���������ĸ���4�ף���������2.8�ף���ô�����ܷ�˳��ͨ����˵�����ɣ���| 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����������������꼶��ѧ ���ͣ�044
��ͼA��������ת��ͼ��ʾ��ת��A��ת��B��ָ�룬(1)������ָ��ͣ����Ӱ�ϣ���ôѡ�ĸ�ת�̳ɹ��ĸ��ʱȽϴ�(2)������ѧ���ֱ�ת��ת��A��ת��B��ת��ֹͣ��ָ��ָ��˳ʱ�����õ�һ�����֣�������յõ���������ż����1�֣����÷֣���������Ϸ����ת��10��ת�̣���¼ÿ�ε÷ֽ�����÷ָ�Ϊʤ�������Ϸ�Լס������˹�ƽ��˵˵���ɣ������ת��A��ת��B������ͼB����״������Ϸ��ƽ��
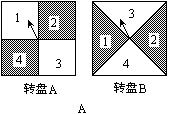

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013�콭�������д��������꼶��ѧ����ĩ������ѧ�Ծ����������� ���ͣ������
����ij��ҵ����һ�ָ����ߣ����Ⱥ��Բ��ƣ�����״����Ϊ�����Σ��߳�x��cm����5~25֮�䣨����5��25����ÿƬ�����ߵijɱ��ۣ�Ԫ�������������cm2������������������P��Ԫ�������ı߳�x��cm������һ�κ�����ͼ����ͼ��ʾ��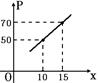
��1����֪����һ�ű߳�Ϊ15cm�ĸ����ߣ���õ�������55Ԫ������=������-�ɱ��ۣ�.
����ÿƬ�ĸ���������Q��Ԫ����߳�x��cm��֮������ĺ�����ϵʽ��
�ڵ��߳�Ϊ����ʱ�������ĸ������ܻ�����������������Ƕ��٣�
��2���ڣ�1���Ļ����ϣ�������Ҽ��������Ʒ��ģ����5cm~25cm����5cm~60cm������20cm~40cm�ĸ��������ڹ��ҿƼ���Ŀ�����Ҷ��ⲿ�ֲ�Ʒ����������ÿƬ����������W��Ԫ�������ı߳�x��cm�����㣺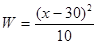 �����ƹ�20cm~40cm�ĸ�����ʱ�����ҽ����г�Ӫ�������ֹ��ĸ����߹���ΪÿƬ10Ԫ��ҪʹÿƬ�����ߵ�������60.4Ԫ����5cm~60cm�ĸ����߱߳�x��ȡֵ��Χ��xȡ��������
�����ƹ�20cm~40cm�ĸ�����ʱ�����ҽ����г�Ӫ�������ֹ��ĸ����߹���ΪÿƬ10Ԫ��ҪʹÿƬ�����ߵ�������60.4Ԫ����5cm~60cm�ĸ����߱߳�x��ȡֵ��Χ��xȡ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012ѧ�������о��꼶3���¿���ѧ�Ծ��������棩 ���ͣ������
�ɽ������ʪ�ع���Ŀǰ��������ʪ�ع����ù����ڶ���ϡ��ֲ��Ͷ��صĵƹ����Ȫ��������Խ��Խ����ο�ǰ�����档Ϊ��Ӧ���ο�����������е������˺�������������״Ϊ��ͼ��ʾ���ı�������㳡����һ������ȡҩ�� ���Ա����������ø���Ӧ��ҩ���Ҫ���ȡҩ���������㳡���
���Ա����������ø���Ӧ��ҩ���Ҫ���ȡҩ���������㳡��� ��
��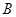 �ľ�����ȣ�������͵�
�ľ�����ȣ�������͵�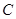 �ľ���ǡ�õ���
�ľ���ǡ�õ���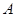 ��
��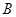 ��ľ��롣����ԭͼ�����ó߹���ͼ����ȡҩ��
��ľ��롣����ԭͼ�����ó߹���ͼ����ȡҩ�� ��λ�á���Ҫ��д��֪�������������ͽ��ۣ�������ͼ�ۼ���������Ǧ����ͼ��
��λ�á���Ҫ��д��֪�������������ͽ��ۣ�������ͼ�ۼ���������Ǧ����ͼ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com