
【题目】你能化简(m﹣1)(m99+m98+…+m+1)吗?遇到这样的复杂问题时,我们可以先从简单的情形入手,探究归纳出一些方法.
(1)分别化简下列各式:
(m﹣1)(m+1)=m2﹣1;
(m﹣1)(m2+m+1)= ;
(m﹣1)(m3+m2+m+1)= ;
(m﹣1)(mn+mn﹣1+mn﹣2+…+m+1)= .
(2)请你利用上面的结论计算:299+298+297+…+2+1,写出计算过程.
(3)根据以上计算经验,直接写出3n+3n﹣1+3n﹣2+…+3+1结果 .
【答案】(1)m3﹣1;m4﹣1;mn+1﹣1;(2)![]() ,计算过程见解析;(3)
,计算过程见解析;(3)![]() .
.
【解析】
(1)根据平方差公式总结规律,即可写出结果;
(2)先对原式变形后,然后再利用得(1)的规律计算即可;
(3)第一个因式:把3-1作为公因式,对原式进行变形,再根据规律解答即可.
解:(1)(m﹣1)(m+1)=m2﹣1;
(m﹣1)(m2+m+1)=m3﹣1;
(m﹣1)(m3+m2+m+1)=m4﹣1;
(m﹣1)(mn+mn﹣1+mn﹣2+…+m+1)=mn+1﹣1;
(2)∵(2﹣1)(299+298+297+…+2+1)=2100﹣1,
∴299+298+297+…+2+1=2100﹣1;
(3)∵(3﹣1)(3n+3n﹣1+3n﹣2+…+3+1)=3n+1﹣1,
∴3n+3n﹣1+3n﹣2+…+3+1=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知A、B、C为数轴上三点,若点C到点A的距离是点C到点B的距离的2倍,则称点C是(A,B)的奇异点,例如图1中,点A表示的数为﹣1,点B表示的数为2,表示1的点C到点A的距离为2,到点B的距离为1,则点C是(A,B)的奇异点,但不是(B,A)的奇异点.
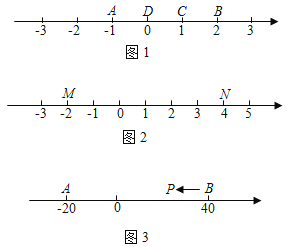
(1)在图1中,直接说出点D是(A,B)还是(B,C)的奇异点;
(2)如图2,若数轴上M、N两点表示的数分别为﹣2和4,
①若(M,N)的奇异点K在M、N两点之间,则K点表示的数是 ;
②若(M,N)的奇异点K在点N的右侧,请求出K点表示的数.
(3)如图3,A、B在数轴上表示的数分别为﹣20和40,现有一点P从点B出发,向左运动.若点P到达点A停止,则当点P表示的数为多少时,P、A、B中恰有一个点为其余两点的奇异点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】省城太原某大型超市计划在12月23日推出“十周年”店庆促销活动,该超市为本次促销活动设计了两种促销方案.方案一:全场商品全部打8.5折;方案二:商品总价不超过200元时,不打折,超过200元时,超过的部分打7折.小颖和爸爸妈妈准备在该超市促销活动期间去该超市购物,所购商品总价一定会超过200元.
(1)小颖和爸爸妈妈购买的商品总价为![]() 元,按方案一应该支付 元;按方案二应该支付 元;(用含
元,按方案一应该支付 元;按方案二应该支付 元;(用含![]() 的代数式表示)
的代数式表示)
(2)当小颖和爸爸妈妈购买的商品总价为多少元时,按方案一或方案二支付的金额都一样?
(3)若小颖和爸爸妈妈购买的商品总价为500元,请你帮助小颖计算一下,按哪种方案支付更划算.
查看答案和解析>>
科目:初中数学 来源: 题型:
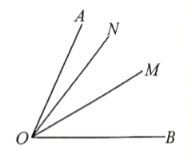
【题目】(1)如图,![]() 的平分线为
的平分线为![]() ,
,![]() 为
为![]() 内的一条射线,若
内的一条射线,若![]() ,
,![]() 时,求
时,求![]() 的度数;
的度数;
(2)某同学经过认真的分析,得出一个关系式:![]() ,你认为这个同学得出的关系式是正确的吗?若正确,请把得出这个结论的过程写出来.
,你认为这个同学得出的关系式是正确的吗?若正确,请把得出这个结论的过程写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
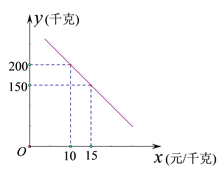
【题目】某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节,已知该蜜柚的成本价为8元/千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)之间的函数关系如图所示.
(元/千克)之间的函数关系如图所示.
(1)求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点D、E分别是边BC、AC的中点,过点A作
中,点D、E分别是边BC、AC的中点,过点A作![]() 交DE的延长线于F点,连接AD、CF.
交DE的延长线于F点,连接AD、CF.
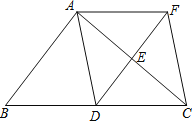
(1)求证:四边形ADCF是平行四边形;
(2)当![]() 满足什么条件时,四边形图ADCF是菱形?为什么?
满足什么条件时,四边形图ADCF是菱形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中进行“选科走班”教学改革,语文、数学、英语三门为必修学科,另外还需从物理、化学、生物、政治、历史、地理(分别记为A、B、C、D、E、F)六门选修学科中任选三门,现对该校某班选科情况进行调查,对调查结果进行了分析统计,并制作了两幅不完整的统计图.
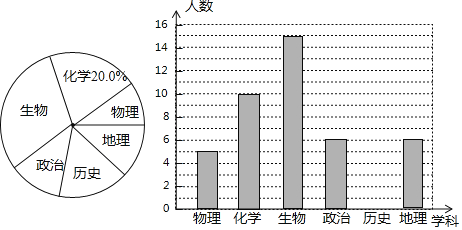
请根据以上信息,完成下列问题:
(1)该班共有学生人;
(2)请将条形统计图补充完整;
(3)该班某同学物理成绩特别优异,已经从选修学科中选定物理,还需从余下选修学科中任意选择两门,请用列表或画树状图的方法,求出该同学恰好选中化学、历史两科的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图点A(1,1),B(2,﹣3),点P为x轴上一点,当|PA﹣PB|最大时,点P的坐标为( )

A. (﹣1,0) B. (![]() ,0) C. (
,0) C. (![]() ,0) D. (1,0)
,0) D. (1,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|,当A、B两点都不在原点时.
(1)如图2,点A、B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=a﹣b=|a﹣b|
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=a﹣b=|a﹣b|
综上,数轴上A、B两点的距离|AB|=|a﹣b|
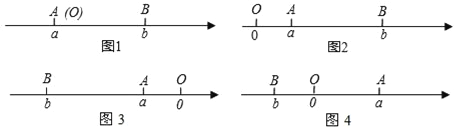
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示﹣2和5的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2那么x为 .
(3)若x表示一个有理数,则|x﹣1|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com