
 设计一个商标图形(如图8所示),在△ABC中,AB=AC=2cm,∠B=30°,以A为圆心,AB为半径作 $\widehat{BEC}$,以BC为直径作半圆$\widehat{BFC}$,则商标图案(阴影)面积等于$\frac{π}{6}$+$\sqrt{3}$cm2.
设计一个商标图形(如图8所示),在△ABC中,AB=AC=2cm,∠B=30°,以A为圆心,AB为半径作 $\widehat{BEC}$,以BC为直径作半圆$\widehat{BFC}$,则商标图案(阴影)面积等于$\frac{π}{6}$+$\sqrt{3}$cm2. 分析 由图可知:图案的面积=半圆CBF的面积+△ABC的面积-扇形ABC的面积,可根据各自的面积计算方法求出图案的面积.
解答 解:∵S扇形ACB=$\frac{120•π•{2}^{2}}{360}$=$\frac{4π}{3}$,S半圆CBF=$\frac{1}{2}$π×($\sqrt{3}$)2=$\frac{3}{2}$π,S△ABC=$\frac{1}{2}$×2$\sqrt{3}$×1=$\sqrt{3}$;
所以图案面积=S半圆CBF+S△ABC-S扇形ACB=$\frac{3}{2}$π+$\sqrt{3}$-$\frac{4}{3}$π=($\frac{π}{6}$+$\sqrt{3}$)cm2,
故答案为:$\frac{π}{6}$+$\sqrt{3}$.
点评 本题主要考查了扇形和三角形的面积计算方法.将不规则图形的面积通常转化为规则图形的面积的和差是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 左拐60° | B. | 右拐60° | C. | 左拐120° | D. | 右拐120° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
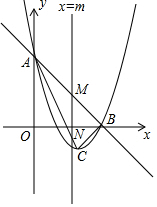 如图,已知抛物线y=x2+bx+c与直线y=-x+3相交于坐标轴上的A,B两点,顶点为C.
如图,已知抛物线y=x2+bx+c与直线y=-x+3相交于坐标轴上的A,B两点,顶点为C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
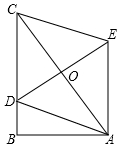 如图,在Rt△ABC中,∠B=90°,∠BAC=60°,AB=1,点D在BC边上,以AC为对角线的平行四边形ADCE中,当DE的长最小时,平行四边形ADCE的面积为$\frac{\sqrt{3}}{2}$.
如图,在Rt△ABC中,∠B=90°,∠BAC=60°,AB=1,点D在BC边上,以AC为对角线的平行四边形ADCE中,当DE的长最小时,平行四边形ADCE的面积为$\frac{\sqrt{3}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com