
 ;
; ,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由; 的最大值.
的最大值.
 =
= ,而已知
,而已知 ,故点O与点Q重合,即点O为△ABC的重心;
,故点O与点Q重合,即点O为△ABC的重心; 的表达式,这是一个二次函数,利用二次函数的性质求出其最大值.
的表达式,这是一个二次函数,利用二次函数的性质求出其最大值.
 AC.
AC. =2,
=2, .
.
 =
= ,
, ,
,
 ,即OA=2OD,
,即OA=2OD, =
= =
= ①
① ,
, CD=
CD= BC;
BC; ,
, ;
; =
= ,
,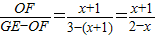 .
. ,
, =
= ,
, ,代入①式得:
,代入①式得: =
= =
= =-x2+x+1=-(x-
=-x2+x+1=-(x- )2+
)2+ ,
, 时,
时, 有最大值,最大值为
有最大值,最大值为 .
. 的关系式是解题的关键;另外,第(3)问尚有多种不同的解法,同学们可以深入探究.
的关系式是解题的关键;另外,第(3)问尚有多种不同的解法,同学们可以深入探究. 

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
| AO |
| AD |
| 2 |
| 3 |
| AO |
| AD |
| 2 |
| 3 |
| S四边形BCHG |
| S△AGH |

查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(四川绵阳卷)数学(解析版) 题型:解答题
(2013年四川绵阳14分)我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心.重心有很多美妙的性质,如关于线段比.面积比就有一些“漂亮”结论,利用这些性质可以解决三角形中的若干问题.请你利用重心的概念完成如下问题:

(1)若O是△ABC的重心(如图1),连结AO并延长交BC于D,证明: ;
;
(2)若AD是△ABC的一条中线(如图2),O是AD上一点,且满足 ,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
(3)若O是△ABC的重心,过O的一条直线分别与AB、AC相交于G、H(均不与△ABC的顶点重合)(如图3),S四边形BCHG,S△AGH分别表示四边形BCHG和△AGH的面积,试探究 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
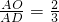 ;
;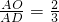 ,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;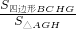 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心。重心有很多美妙的性质,如在关线段比.面积比就有一些“漂亮”结论,利用这些性质可以解决三角形中的若干问题。请你利用重心的概念完成如下问题:
(1)若O是△ABC的重心(如图1),连结AO并延长交BC于D,证明:![]() ;
;
(2)若AD是△ABC的一条中线(如图2),O是AD上一点,且满足![]() ,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
(3)若O是△ABC的重心,过O的一条直线分别与AB、AC相交于G、H(均不与△ABC的顶点重合)(如图3),S四边形BCHG.S△AGH分别表示四边形BCHG和△AGH的面积,试探究![]() 的最大值。
的最大值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com