
 如图,一幢大楼的顶部竖有一块写有“校训”的宣传牌CD.小明在山坡的底部A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB垂直于视线AD,AB=20米,AE=30米,则这块宣传牌CD的高度为5.4米.(测角器的高度忽略不计,结果精确到0.1米.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,一幢大楼的顶部竖有一块写有“校训”的宣传牌CD.小明在山坡的底部A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB垂直于视线AD,AB=20米,AE=30米,则这块宣传牌CD的高度为5.4米.(测角器的高度忽略不计,结果精确到0.1米.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732). 分析 过B分别作AE、DE的垂线,设垂足为F、G.分别在Rt△ABF和Rt△ADE中,通过解直角三角形求出BF、AF、DE的长,进而可求出EF即BG的长;在Rt△CBG中,∠CBG=45°,则CG=BG,由此可求出CG的长;根据CD=CG+GE-DE即可求出宣传牌的高度.
解答 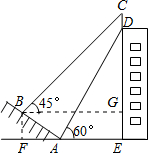 解:过B作BF⊥AE,交EA的延长线于F,作BG⊥DE于G.
解:过B作BF⊥AE,交EA的延长线于F,作BG⊥DE于G.
Rt△ABF中,∵∠AFB=90°,∠BAF=180°-60°-90°=30°,
∴BF=$\frac{1}{2}$AB=10,AF=$\sqrt{3}$BF=10$\sqrt{3}$,
∴BG=AF+AE=10$\sqrt{3}$+30.
在Rt△BGC中,∵∠BGC=90°,∠CBG=45°,
∴CG=BG=10$\sqrt{3}$+30.
Rt△ADE中,∵∠AED=90°,∠DAE=60°,AE=30,
∴DE=$\sqrt{3}$AE=30$\sqrt{3}$,
∴CD=CG+GE-DE=10$\sqrt{3}$+30+10-30$\sqrt{3}$≈5.4.
答:宣传牌CD高约5.4米.
故答案为5.4米.
点评 此题考查了解直角三角形的应用-仰角俯角问题,能够正确地构建出直角三角形,将实际问题化归为解直角三角形的问题是解答此类题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:填空题
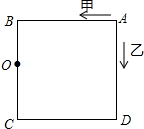 在某个奔跑活动中,有一个边长为10m正方形路线图,两名选手甲,乙同时从起点A沿着箭头方向绕路线图奔跑,两人第一次相遇在BC的中点O处,当两名选手第一次在点A处相遇时,选手乙已经跑了200m.
在某个奔跑活动中,有一个边长为10m正方形路线图,两名选手甲,乙同时从起点A沿着箭头方向绕路线图奔跑,两人第一次相遇在BC的中点O处,当两名选手第一次在点A处相遇时,选手乙已经跑了200m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,是一副普通扑克牌中的13张黑桃牌.将它们洗匀后正面向下放在桌子上,从中任意抽取一张,则抽出的牌点数小于8的概率为$\frac{7}{13}$.
如图,是一副普通扑克牌中的13张黑桃牌.将它们洗匀后正面向下放在桌子上,从中任意抽取一张,则抽出的牌点数小于8的概率为$\frac{7}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
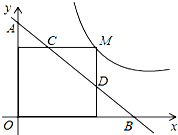 如图,M为双曲线y=$\frac{2}{3x}$(x>0)上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点.若直线y=-x+m与y轴交于点A,与x轴交于点B,则AD•BC的值为$\frac{4}{3}$.
如图,M为双曲线y=$\frac{2}{3x}$(x>0)上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点.若直线y=-x+m与y轴交于点A,与x轴交于点B,则AD•BC的值为$\frac{4}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com