
 如图,点B、E、C、F在同一直线上,AB=DE,∠ABC=∠DEF,BE=CF,求证:AC∥DF.
如图,点B、E、C、F在同一直线上,AB=DE,∠ABC=∠DEF,BE=CF,求证:AC∥DF.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
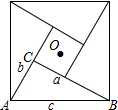 在Rt△ABC中,∠ACB=90°,BC=a,AC=b.AB=c,将Rt△ABC绕点O依次旋转90°、180°和270°,构成的图形如图所示,该图是我国古代数学家赵爽制作的“勾股圆方图”,也被称作“赵爽弦图”,它是我国最早对勾股定理证明的记载,也成为了2002年在北京召开的国际数学家大会的会标设计的主要依据.
在Rt△ABC中,∠ACB=90°,BC=a,AC=b.AB=c,将Rt△ABC绕点O依次旋转90°、180°和270°,构成的图形如图所示,该图是我国古代数学家赵爽制作的“勾股圆方图”,也被称作“赵爽弦图”,它是我国最早对勾股定理证明的记载,也成为了2002年在北京召开的国际数学家大会的会标设计的主要依据.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com