【题目】已知如图：AD∥BC，E、F分别在DC、AB延长线上.∠DCB=∠DAB，AE⊥EF，∠DEA=30°.
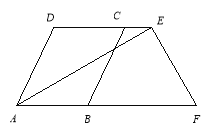
(1)、求证：DC//AB. (2)、求∠AFE的大小.
【答案】(1)、证明过程见解析；(2)、60°
【解析】
试题分析：(1)、根据AD∥BC得出∠ABC+∠DAB=180°，根据∠DCB=∠DAB得出∠ABC+∠DCB=180°，从而得出直线平行；(2)、根据AE⊥EF得出∠AEF=90°，从而说明∠DEF=120°，根据平行线的性质得出∠AFE的度数.
试题解析：（1）∵AD//BC ∴∠ABC+∠DAB=180°° ∵∠DCB=∠DAB ∴∠ABC+∠DCB=180° ∴DC//AB；
(2)、∵AE⊥EF, ∴∠AEF=90° ∵∠DEA=30° ∴∠DEF=30°+ 90° =120° ∵DC//AB
∴∠DEF+∠F=180° ∴∠AFE=60°
科学实验活动册系列答案科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，一个点从A（a1，a2）出发沿图中路线依次经过B（a3，a4），C（a5，a6），D（a7，a8），…，按此一直运动下去，则a2015+a2016的值为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算或化简（整式乘法）
(1). （-3ab)· (- 4b）2 ； (2).
.
(3). 3x(x2-2x-1)+6x (4).
+(-x+1)(x-2)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 填空题：如图，AB//CD，∠ABC=50°，∠CPN=150°，∠PNB=60°，∠NDC=60°，求∠BCP的度数。
解：
，（已知）
，（等量代换）
PN // CD，（ ）
_________=180°，（ ）
，（已知）
，（已知）
____________，（两直线平行，内错角相等）
，（已知）
__________，（等量代换）
BCP=BCD－PCD=____________°－30°=_________°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
