
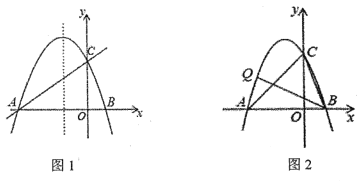
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线![]() ,且抛物线经过B(1,0),C(0,3)两点,与x轴交于点A.
,且抛物线经过B(1,0),C(0,3)两点,与x轴交于点A.
(1)求抛物线的解析式;
(2)如图1,在抛物线的对称轴直线![]() 上找一点M,使点M到点B的距离与到点C的距离之和最小,求出点M的坐标;
上找一点M,使点M到点B的距离与到点C的距离之和最小,求出点M的坐标;
(3)如图2,点Q为直线AC上方抛物线上一点,若∠CBQ=45°,请求出点Q坐标.
【答案】(1)![]() ;(2)当点
;(2)当点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小时
的距离之和最小时![]() 的坐标为
的坐标为![]() ;(3)点
;(3)点![]() .
.
【解析】
(1)根据对称轴方程可得![]() ,把B、C坐标代入列方程组求出a、b、c的值即可得答案;
,把B、C坐标代入列方程组求出a、b、c的值即可得答案;
(2)根据二次函数的对称性可得A点坐标,设直线AC与对称轴![]() 的交点为M,可得MB=MA,即可得出MB+MC=MC+MA=AC,为MB+MC的最小值,根据A、C坐标,利用待定系数法可求出直线AC的解析式,把x=-1代入求出y值,即可得点M的坐标.
的交点为M,可得MB=MA,即可得出MB+MC=MC+MA=AC,为MB+MC的最小值,根据A、C坐标,利用待定系数法可求出直线AC的解析式,把x=-1代入求出y值,即可得点M的坐标.
(3)设直线BQ交y轴于点H,过点![]() 作
作![]() 于点
于点![]() ,利用勾股定理可求出BC的长,根据∠CBQ=45°可得HM=BM,利用∠OCB的正切函数可得CM=3HM,即可求出CM、HM的长,利用勾股定理可求出CH的长,即可得H点坐标,利用待定系数法可得直线BH的解析式,联立直线BQ与抛物线的解析式求出交点坐标即可得点Q坐标.
,利用勾股定理可求出BC的长,根据∠CBQ=45°可得HM=BM,利用∠OCB的正切函数可得CM=3HM,即可求出CM、HM的长,利用勾股定理可求出CH的长,即可得H点坐标,利用待定系数法可得直线BH的解析式,联立直线BQ与抛物线的解析式求出交点坐标即可得点Q坐标.
(1)∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线![]() ,
,
∴![]() ,
,
∵抛物线经过B(1,0),C(0,3)两点,
∴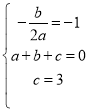 ,
,
解得: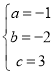 ,
,
∴抛物线解析式为![]() .
.
(2)设直线AC的解析式为y=mx+n,
∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线![]() ,B(0,0),
,B(0,0),
∴点A坐标为(-3,0),
∵C(0,3),
∴![]() ,
,
解得:![]() ,
,
∴直线解析式为![]() ,
,
设直线![]() 与对称轴
与对称轴![]() 的交点为
的交点为![]() ,
,
∵点A与点B关于对称轴x=-1对称,
∴MA=MB,
∴MB+MC=MA+MC=AC,
∴此时![]() 的值最小,
的值最小,
当![]() 时,y=-1+3=2,
时,y=-1+3=2,
∴当点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小时
的距离之和最小时![]() 的坐标为
的坐标为![]() .
.
(3)如图,设直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
∵B(1,0),C(0,3),
∴OB=1,OC=3,BC=![]() =
=![]() ,
,
∴![]() ,
,
∵∠CBQ=45°,
∴△BHM是等腰直角三角形,
∴HM=BM,
∵tan∠OCB=![]() ,
,
∴CM=3HM,
∴BC=MB+CM=4HM=![]() ,
,
解得:![]() ,
,
∴CM=![]() ,
,
∴CH=![]() =
=![]() ,
,
∴OH=OC-CH=3-![]() =
=![]() ,
,
∴![]() ,
,
设直线BH的解析式为:y=kx+b,
∴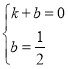 ,
,
解得: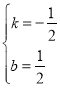 ,
,
∴![]() 的表达式为:
的表达式为:![]() ,
,
联立直线BH与抛物线解析式得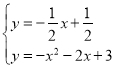 ,
,
解得:![]() (舍去)或x=
(舍去)或x=![]() ,
,
当x=![]() 时,y=
时,y=![]() =
=![]() ,
,
∴点Q坐标为(![]() ,
,![]() ).
).



科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0,a、b、c为常数)上部分点的横坐标x,纵坐标y的对应值如下表:
x | …… | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | …… |
y | …… |
| 4 |
| 4 | m | 0 | …… |
则下列结论中:①抛物线的对称轴为直线x=﹣1;②m=![]() ;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0),则下面的四个结论,其中正确的个数为( )
①2a+b=0②4a﹣2b+c<0③ac>0④当y>0时,﹣1<x<4
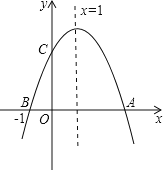
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强中学生体质,篮球运球已列为铜陵市体育中考选考项目,某校学生不仅练习运球,还练习了投篮,下表是一名同学在罚球线上投篮的试验结果,根据表中数据,回答问题.
投篮次数(n) | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
投中次数(m) | 28 | 60 | 78 | 104 | 124 | 153 | 252 |
(1)估计这名同学投篮一次,投中的概率约是多少?(精确到0.1)
(2)根据此概率,估计这名同学投篮622次,投中的次数约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2019大洋湾盐城马拉松”的赛事共有三项:A,“全程马拉松”、B,“半程马拉松”、C.“迷你健身跑”,小明和小刚参与了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.
(1)小明被分配到“迷你健身跑”项目组的概率为 ;
(2)求小明和小刚被分配到不同项目组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组为测量一棵古树BH和教学楼![]() 的高,先在点
的高,先在点![]() 处用高1.5米的测角仪测得古树顶端点
处用高1.5米的测角仪测得古树顶端点![]() 的仰角
的仰角![]() 为
为![]() ,此时教学楼顶端点
,此时教学楼顶端点![]() 恰好在视线
恰好在视线![]() 上,再向前走7米到达点
上,再向前走7米到达点![]() 处,又测得教学楼顶端点
处,又测得教学楼顶端点![]() 的仰角
的仰角![]() 为
为![]() ,点
,点![]() 、
、![]() 、
、![]() 点在同一水平线上.
点在同一水平线上.
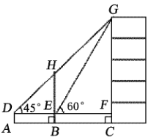
(1)计算古树![]() 的高度;
的高度;
(2)计算教学楼![]() 的高度.(结果精确到0.1米,参考数据:
的高度.(结果精确到0.1米,参考数据:![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号手机进价多500元,若商场用50000元共购进A型号手机10部,B型号手机20部,求A、B两种型号的手机每部进价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菲尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,颁给有卓越贡献的年轻数学家,被视为数学界的诺贝尔奖.下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄(岁):39 35 33 39 27 33 35 31 31 37 32 38 36 31 39 32 38 37 34 34 38 32 35 36 33 32 35 36 37 39 38 40 38 37 39 38 34 33 40 36 36 37 31 38 38 37 35 40 39 37
请根据以上数据,解答以下问题:
(1)小彬按“组距为5”列出了如下的频数分布表,每组数据含最小值不含最大值,请将表中空缺的部分补充完整,并补全频数分布直方图:
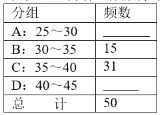
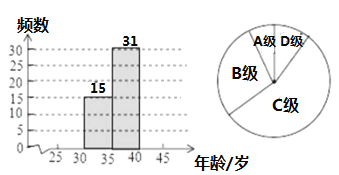
(2)在(1)的基础上,小彬又画出了如图所示的扇形统计图,图中B组所对的圆心角的度数为 ;
(3)根据(1)中的频数分布直方图试描述这50位菲尔兹奖得主获奖时的年龄的分布特征.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com