
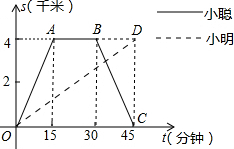
 小聪和小明沿同一条路同时从学校出发到某超市购物,学校与超市的路程是4千米.小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达超市.图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
小聪和小明沿同一条路同时从学校出发到某超市购物,学校与超市的路程是4千米.小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达超市.图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:分析 (1)根据购物时间=离开时间-到达时间即可求出小聪在超市购物的时间;再根据速度=路程÷时间即可算出小聪返回学校的速度;
(2)根据点的坐标利用待定系数法即可求出小明离开学校的路程s与所经过的时间t之间的函数关系式;
(3)根据点的坐标利用待定系数法即可求出当30≤s≤45时小聪离开学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系式,令两函数关系式相等即可得出关于t的一元一次方程,解之即可求出t值,再将其代入任意一函数解析式求出s值即可.
解答 解:(1)30-15=15(分钟);
4÷(45-30)=$\frac{4}{15}$(千米/分钟).
故答案为:15;$\frac{4}{15}$.
(2)设小明离开学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系式为s=mt+n,
将(0,0)、(45,4)代入s=mt+n中,
$\left\{\begin{array}{l}{n=0}\\{45m+n=4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=\frac{4}{45}}\\{n=0}\end{array}\right.$,
∴s=$\frac{4}{45}$t.
∴小明离开学校的路程s与所经过的时间t之间的函数关系式为s=$\frac{4}{45}$t.
(3)当30≤s≤45时,设小聪离开学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系式为s=kt+b,
将(30,4)、(45,0)代入s=kt+b,
$\left\{\begin{array}{l}{30k+b=4}\\{45k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{4}{15}}\\{b=12}\end{array}\right.$,
∴s=-$\frac{4}{15}$t+12.
令s=$\frac{4}{45}$t=-$\frac{4}{15}$t+12,
解得:t=$\frac{135}{4}$,
∴s=$\frac{4}{45}$t=$\frac{4}{45}$×$\frac{135}{4}$=3.
答:当小聪与小明迎面相遇时,他们离学校的路程是3千米.
点评 本题考查了一次函数的应用以及待定系数法求一次函数解析式,解题的关键是:(1)根据数量关系列式计算;(2)根据点的坐标利用待定系数法求出函数关系式;(3)根据点的坐标利用待定系数法求出函数关系式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
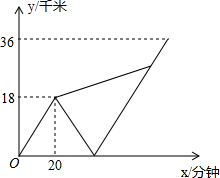 甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为t(分钟).y甲、y乙与x之间的函数图象如图所示,则乙返回到学校时,甲与学校相距20千米.
甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为t(分钟).y甲、y乙与x之间的函数图象如图所示,则乙返回到学校时,甲与学校相距20千米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知∠1=∠2,∠4=∠5,∠3=∠E,试说明AE∥BD,AD∥BC,请完成下列证明过程.
如图,已知∠1=∠2,∠4=∠5,∠3=∠E,试说明AE∥BD,AD∥BC,请完成下列证明过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com