Question

如图，已知正方形ABCD，点E是BC上一点，以AE为边作正方形AEFG。

（1）连结GD，求证△ADG≌△ABE；
（2）连结FC，求证∠FCN=45°；
（3）请问在AB边上是否存在一点Q，使得四边形DQEF是平行四边形？若存在，请证明；若不存在，请说明理由。

Answer 1

（1）根据同角的余角相等得∠DAG=∠BAE，再根据“SAS”证得△ADG≌△ABE；（2）过F作BN的垂线，设垂足为H，首先证△ABE、△EHF全等，然后得AB=EH，BE=FH；然后根据AB=BC=EH，即BE+EC=EC+CH，得到CH=BE=FH，即可证得结果；（3）存在
（3）在AB上取AQ=BE，连接QD，首先证△DAQ、△ABE、△ADG三个三角形全等，易证得AG、QD平行且相等，又由于AG、EF平行且相等，所以QD、EF平行且相等，即可得证．

试题分析：（1）根据同角的余角相等得∠DAG=∠BAE，再根据“SAS”证得△ADG≌△ABE；
（2）过F作BN的垂线，设垂足为H，首先证△ABE、△EHF全等，然后得AB=EH，BE=FH；然后根据AB=BC=EH，即BE+EC=EC+CH，得到CH=BE=FH，即可证得结果；
（3）在AB上取AQ=BE，连接QD，首先证△DAQ、△ABE、△ADG三个三角形全等，易证得AG、QD平行且相等，又由于AG、EF平行且相等，所以QD、EF平行且相等，即可证得结果．
（1）如图

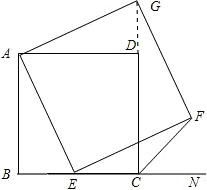
∵四边形ABCD和四边形AEFG是正方形
∴DA=BA，EA=GA，∠BAD=∠EAG=90°
∴∠DAG=∠BAE
∴△ADG≌△ABE；
（2）过F作BN的垂线，设垂足为H

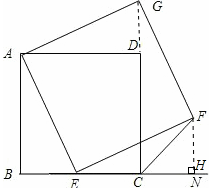
∵∠BAE+∠AEB=90°，∠FEH+∠AEB=90°
∴∠BAE=∠HEF
∵AE=EF
∴△ABE≌△EHF
∴AB=EH，BE=FH
∴AB=BC=EH
∴BE+EC=EC+CH
∴CH=BE=FH
∴∠FCN=45°；
（3）在AB上取AQ=BE，连接QD

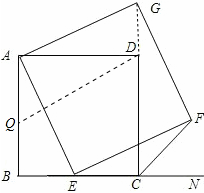
∵AB=AD
∴△DAQ≌△ABE
∵△ABE≌△EHF
∴△DAQ≌△ABE≌△ADG
∴∠GAD=∠ADQ
∴AG、QD平行且相等
又∵AG、EF平行且相等
∴QD、EF平行且相等
∴四边形DQEF是平行四边形
∴在AB边上存在一点Q，使得四边形DQEF是平行四边形．
点评：本题知识点较多，难度较大，熟练掌握平面图形的基本概念是解答本题的关键.