
”¾ĢāÄæ”æČēĶ¼£¬Ņ»“ĪŗÆŹż![]() µÄĶ¼ĻóÓė¶ž“ĪŗÆŹż
µÄĶ¼ĻóÓė¶ž“ĪŗÆŹż![]() µÄĶ¼Ļó½»ÓŚ×ų±źÖįÉĻµÄ
µÄĶ¼Ļó½»ÓŚ×ų±źÖįÉĻµÄ![]() Į½µć£®
Į½µć£®
£Ø1£©Ē󶞓ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©µć![]() ŹĒÖ±Ļß
ŹĒÖ±Ļß![]() ÉĻ·½Å×ĪļĻßÉĻŅ»µć£¬¹żµć
ÉĻ·½Å×ĪļĻßÉĻŅ»µć£¬¹żµć![]() ·Ö±š×÷
·Ö±š×÷![]() Öį
Öį![]() ÖįĘ½ŠŠĻß·Ö±š½»Ö±Ļß
ÖįĘ½ŠŠĻß·Ö±š½»Ö±Ļß![]() ÓŚµć
ÓŚµć![]() ŗĶµć
ŗĶµć![]() £¬Éčµć
£¬Éčµć![]() µÄŗį×ų±źĪŖ
µÄŗį×ų±źĪŖ![]() £¬ĒėÓĆŗ¬
£¬ĒėÓĆŗ¬![]() µÄ“śŹżŹ½±ķŹ¾
µÄ“śŹżŹ½±ķŹ¾![]() µÄÖܳ¤£¬²¢Ēó³öµ±
µÄÖܳ¤£¬²¢Ēó³öµ±![]() µÄÖܳ¤Č”µĆ×ī“óÖµ(²»ŠčŅŖĒó³ö“Ė×ī“óÖµ)Ź±µć
µÄÖܳ¤Č”µĆ×ī“óÖµ(²»ŠčŅŖĒó³ö“Ė×ī“óÖµ)Ź±µć![]() µÄ×ų±ź£»
µÄ×ų±ź£»
£Ø3£©µć![]() ŹĒÖ±Ļß
ŹĒÖ±Ļß![]() ÉĻŅ»µć£¬µć
ÉĻŅ»µć£¬µć![]() ŹĒÅ×ĪļĻßÉĻŅ»µć£¬ŌŚµŚ¶žĪŹ
ŹĒÅ×ĪļĻßÉĻŅ»µć£¬ŌŚµŚ¶žĪŹ![]() µÄÖܳ¤Č”µĆ×ī“óÖµµÄĢõ¼žĻĀ£¬ĒėÖ±½ÓŠ“³öŹ¹ŅŌµć
µÄÖܳ¤Č”µĆ×ī“óÖµµÄĢõ¼žĻĀ£¬ĒėÖ±½ÓŠ“³öŹ¹ŅŌµć![]() ĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪµÄµć
ĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪµÄµć![]() µÄ×ų±ź£®
µÄ×ų±ź£®
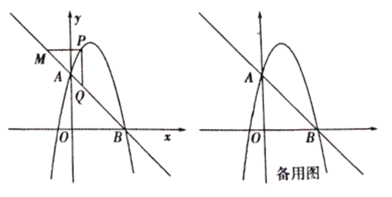
”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©Öܳ¤
£»£Ø2£©Öܳ¤![]() £¬
£¬![]() £»£Ø3£©µć
£»£Ø3£©µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() »ņ
»ņ![]()
”¾½āĪö”æ
£Ø1£©ĻČĄūÓĆŅ»“ĪŗÆŹż½āĪöŹ½£¬Ēó³öA£¬B×ų±ź£¬ŌŁ“śČė![]() £¬Ēó³öb£¬c¼“æɵƵ½¶ž“ĪŗÆŹż½āĪöŹ½£»
£¬Ēó³öb£¬c¼“æɵƵ½¶ž“ĪŗÆŹż½āĪöŹ½£»
£Ø2£©Éčµć![]() £¬æÉµĆ³öPQµÄ±ķ“ļŹ½£¬Ņ×Ö¤
£¬æÉµĆ³öPQµÄ±ķ“ļŹ½£¬Ņ×Ö¤![]() ĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬¼“æÉµĆ³ö
ĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬¼“æÉµĆ³ö![]() £¬ŌŁĄūÓƶž“ĪŗÆŹżµÄŠŌÖŹæÉµĆ³öÖܳ¤×ī“óŹ±MµÄ×ų±ź£»
£¬ŌŁĄūÓƶž“ĪŗÆŹżµÄŠŌÖŹæÉµĆ³öÖܳ¤×ī“óŹ±MµÄ×ų±ź£»
£Ø3£©Éč![]() £¬
£¬![]() £¬øł¾ŻĘ½ŠŠĖıߊĪ¶Ō½ĒĻß»„ĻąĘ½·ÖµÄŠŌÖŹ£¬·Ö±šĢÖĀŪPC£¬PQ£¬PDĪŖ¶Ō½ĒĻߣ¬½ØĮ¢·½³ĢĒó½ā£®
£¬øł¾ŻĘ½ŠŠĖıߊĪ¶Ō½ĒĻß»„ĻąĘ½·ÖµÄŠŌÖŹ£¬·Ö±šĢÖĀŪPC£¬PQ£¬PDĪŖ¶Ō½ĒĻߣ¬½ØĮ¢·½³ĢĒó½ā£®
½ā£ŗ£Ø1£©Įī![]() ÖŠ
ÖŠ![]() ĪŖ0µĆy=4£¬Ōņ
ĪŖ0µĆy=4£¬Ōņ![]() £¬
£¬
Įīy=0£¬µĆ![]() £¬½āµĆ
£¬½āµĆ![]() £¬Ōņ
£¬Ōņ![]()
·Ö±š½«µć![]() µÄ×ų±ź“śČĖµ½
µÄ×ų±ź“śČĖµ½![]() £¬
£¬
µĆ![]() £¬½āµĆ
£¬½āµĆ![]()
”ą¶ž“ĪŗÆŹżµÄ½āĪöŹ½ĪŖ![]() £®
£®
£Ø2£©ÓÉĢāŅāÉčµć![]() £¬
£¬
Ōņ![]() £®
£®
”ß![]() £¬
£¬
”ą![]() £¬
£¬
”ß![]() Öį£¬
Öį£¬ ![]() Öį£¬
Öį£¬
”ą![]() £¬¼“
£¬¼“![]() ĪŖµČŃüÖ±½ĒČż½ĒŠĪ£®
ĪŖµČŃüÖ±½ĒČż½ĒŠĪ£®
Éč![]() µÄÖܳ¤ĪŖ
µÄÖܳ¤ĪŖ![]() £¬Ōņ
£¬Ōņ![]() £¬
£¬
¼“![]() £®
£®
µ±![]() Ź±£¬
Ź±£¬![]() µÄÖܳ¤Č”µĆ×ī“óÖµ£¬
µÄÖܳ¤Č”µĆ×ī“óÖµ£¬
½«![]() “śČėµ½
“śČėµ½![]() ÖŠæÉµĆ£¬
ÖŠæÉµĆ£¬![]() £¬
£¬
”ą![]() £¬
£¬
”ß![]() Öį£¬
Öį£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]()
£Ø3£©Éč![]() £¬
£¬![]() £¬
£¬
ŌŚ£Ø2£©µÄĢõ¼žĻĀPµć×ų±źĪŖ![]() £¬Qµć×ų±źĪŖ
£¬Qµć×ų±źĪŖ![]()
¢Łµ±PCĪŖ¶Ō½ĒĻߏ±£¬
![]() £¬½āµĆ
£¬½āµĆ![]()
“ĖŹ±C![]() ÓėQµćÖŲŗĻ£¬²»·ūŗĻĢāŅā£¬ÉįČ„£»
ÓėQµćÖŲŗĻ£¬²»·ūŗĻĢāŅā£¬ÉįČ„£»
¢Śµ±PQĪŖ¶Ō½ĒĻߏ±£¬
![]() £¬½āµĆ
£¬½āµĆ![]()
“ĖŹ±C![]() ÓėQµćÖŲŗĻ£¬²»·ūŗĻĢāŅā£¬ÉįČ„£»
ÓėQµćÖŲŗĻ£¬²»·ūŗĻĢāŅā£¬ÉįČ„£»
¢Ūµ±PDĪŖ¶Ō½ĒĻߏ±£¬
![]() £¬½āµĆ
£¬½āµĆ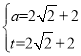 »ņ
»ņ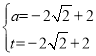
µ±![]() Ź±£¬
Ź±£¬![]() £¬¼“
£¬¼“![]()
µ±![]() Ź±£¬
Ź±£¬![]() £¬¼“
£¬¼“![]()
×ŪÉĻ£¬µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() »ņ
»ņ![]() £®
£®


 æĪŹ±ŃµĮ·½ĖÕČĖĆń³ö°ęÉēĻµĮŠ“š°ø
æĪŹ±ŃµĮ·½ĖÕČĖĆń³ö°ęÉēĻµĮŠ“š°ø »ĘøŌ¾µäȤĪ¶æĪĢĆĻµĮŠ“š°ø
»ĘøŌ¾µäȤĪ¶æĪĢĆĻµĮŠ“š°ø Ęō¶«Š”Ģā×÷Ņµ±¾ĻµĮŠ“š°ø
Ęō¶«Š”Ģā×÷Ņµ±¾ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
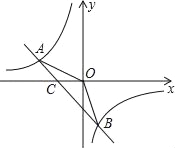
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖA£Ø©4£¬n£©£¬B£Ø2£¬©4£©ŹĒŅ»“ĪŗÆŹży£½kx+bµÄĶ¼ĻóŗĶ·“±ČĄżŗÆŹży£½![]() µÄĶ¼ĻóµÄĮ½øö½»µć£®
µÄĶ¼ĻóµÄĮ½øö½»µć£®
£Ø1£©Ē󷓱ȥżŗÆŹżŗĶŅ»“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©ĒóÖ±ĻßABÓėxÖįµÄ½»µćCµÄ×ų±ź¼°”÷AOBµÄĆ껿£»
£Ø3£©Ö±½ÓŠ“³öŅ»“ĪŗÆŹżµÄÖµŠ”ÓŚ·“±ČĄżŗÆŹżÖµµÄxµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷AB£®CÄŚ½ÓÓŚ”Ń0£¬µćDŌŚ°ė¾¶OBµÄŃÓ³¤ĻßÉĻ£¬”ĻBCD=”ĻA=30”ć£®
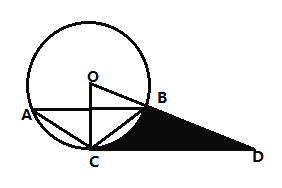
£Ø1£©ÅŠ¶ĻÖ±ĻßCDÓė”Ń0µÄĪ»ÖĆ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ
£Ø2£©Čō”Ń0µÄ°ė¾¶ĪŖ1£¬ĒóŅõÓ°²æ·ÖĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
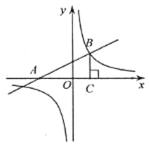
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖŅ»“ĪŗÆŹż![]() µÄĶ¼ĻóÓė
µÄĶ¼ĻóÓė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() £¬Óė·“±ČĄżŗÆŹż
£¬Óė·“±ČĄżŗÆŹż![]() µÄĶ¼ĻóµÄ½»µćĪŖ
µÄĶ¼ĻóµÄ½»µćĪŖ![]() £¬
£¬![]() Öį“¹×ćĪŖ
Öį“¹×ćĪŖ![]() £¬Čōµć
£¬Čōµć![]() ŌŚ·“±ČĄżŗÆŹżĶ¼ĻóÉĻ£¬ĒŅ
ŌŚ·“±ČĄżŗÆŹżĶ¼ĻóÉĻ£¬ĒŅ![]() µÄĆ껿µČÓŚ12£¬Ōņµć
µÄĆ껿µČÓŚ12£¬Ōņµć![]() µÄ×ų±źĪŖ__________.
µÄ×ų±źĪŖ__________.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬![]() ŹĒ
ŹĒ![]() µÄÖ±¾¶£¬µć
µÄÖ±¾¶£¬µć![]() ŹĒŌ²ÉĻ²»Óėµć
ŹĒŌ²ÉĻ²»Óėµć![]() ÖŲŗĻµÄ¶Æµć£¬Į¬½Ó
ÖŲŗĻµÄ¶Æµć£¬Į¬½Ó![]() ²¢ŃÓ³¤µ½µć
²¢ŃÓ³¤µ½µć![]() £¬Ź¹
£¬Ź¹![]() £¬µć
£¬µć![]() ŹĒ
ŹĒ![]() µÄÖŠµć£¬Į¬½Ó
µÄÖŠµć£¬Į¬½Ó![]() £®
£®
£Ø1£©ĒóÖ¤£ŗ![]() £»
£»
£Ø2£©ĢīæÕ£ŗ¢ŁČō![]() £¬µ±
£¬µ±![]() Ź±£¬ĖıߊĪ
Ź±£¬ĖıߊĪ![]() ŹĒĮāŠĪ£»
ŹĒĮāŠĪ£»
¢Śµ±ĖıߊĪ![]() ŹĒÕż·½ŠĪŹ±£¬
ŹĒÕż·½ŠĪŹ±£¬ ![]() ________”ć
________”ć

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬DĪŖ±ßBCÉĻŅ»µć£¬ŅŌAB£¬BDĪŖĮŚ±ß×÷ABDE£¬Į¬½ÓAD£¬EC£®
£Ø1£©ĒóÖ¤£ŗ”÷ADC”Õ”÷ECD£»
£Ø2£©ČōBD=CD£¬ĒóÖ¤£ŗĖıߊĪADCEŹĒ¾ŲŠĪ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æѧĻ°Ķź·“±ČĄżŗÆŹżµÄĶ¼Ļó¼°ŠŌÖŹŗó£¬ĄĻŹ¦øųÕѧĆĒĮōĮĖÕāŃłŅ»µĄ×÷ŅµĢā£ŗ”°ŅŃÖŖµć(©1£¬m)ŗĶµć(2£¬n)¶¼ŌŚ·“±ČĄżŗÆŹży£½![]() £Øk£¼0£©µÄĶ¼ĻóÉĻ£¬ŹŌ±Č½ĻmŗĶnµÄ“󊔣攱ŅŌĻĀŹĒ±ņ±ņĶ¬Ń§µÄ½āĢā¹ż³Ģ£ŗ
£Øk£¼0£©µÄĶ¼ĻóÉĻ£¬ŹŌ±Č½ĻmŗĶnµÄ“󊔣攱ŅŌĻĀŹĒ±ņ±ņĶ¬Ń§µÄ½āĢā¹ż³Ģ£ŗ
½ā£ŗ”ßŌŚ·“±ČĄżŗÆŹży£½![]() ÖŠ£¬k£¼0 ¢Ł
ÖŠ£¬k£¼0 ¢Ł
”ą·“±ČĄżŗÆŹży£½![]() £¬yĖęxµÄŌö“ó¶ųŌö“ó ¢Ś
£¬yĖęxµÄŌö“ó¶ųŌö“ó ¢Ś
”ß![]() ¢Ū
¢Ū
”ą![]() ¢Ü
¢Ü
£Ø1£©±ņ±ņµÄ½ā“š¹ż³ĢŌŚµŚ”” ””²½æŖŹ¼³ö“ķ£¬³ö“ķµÄŌŅņŹĒ”” ””£®ĒėÄć°ļÖś±ņ±ņŠ“³öÕżČ·µÄ½ā“š¹ż³Ģ£®
£Ø2£©Čōµć£Ø©6£¬p£©”¢µć£Ø1£¬q£©ŗĶµć£Ø3£¬z£©Ņ²ŌŚ·“±ČĄżŗÆŹży£½![]() £Øk£¼0£©µÄĶ¼ĻóÉĻ£¬Ö±½Ó±Č½Ļp”¢q”¢zµÄ“óŠ””” ””£Ø½į¹ūÓĆ”°£¼”±Į¬½į£©
£Øk£¼0£©µÄĶ¼ĻóÉĻ£¬Ö±½Ó±Č½Ļp”¢q”¢zµÄ“óŠ””” ””£Ø½į¹ūÓĆ”°£¼”±Į¬½į£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬½«”÷ABCŃŲBC±ßÉĻµÄÖŠĻßADĘ½Ņʵ½”÷A'B'C'µÄĪ»ÖĆ£¬ŅŃÖŖ”÷ABCµÄĆ껿ĪŖ9£¬ŅõÓ°²æ·ÖČż½ĒŠĪµÄĆ껿ĪŖ4£®ČōAA'=1£¬ŌņA'DµČÓŚ£Ø””””£©

A. 2 B. 3 C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
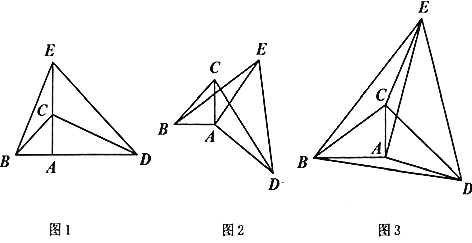
”¾ĢāÄæ”æČēĶ¼![]() £¬ŌŚ
£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() ŹĒ±ß
ŹĒ±ß![]() ÉĻČĪŅāŅ»µć(µć
ÉĻČĪŅāŅ»µć(µć![]() Óėµć
Óėµć![]() ”¢
”¢![]() ²»ÖŲŗĻ)£¬ŅŌ
²»ÖŲŗĻ)£¬ŅŌ![]() ĪŖŅ»Ö±½Ē±ßŌŚ
ĪŖŅ»Ö±½Ē±ßŌŚ![]() µÄĶā²æ×÷
µÄĶā²æ×÷![]() £¬
£¬![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬
£¬![]() £®
£®
£Ø1£©ŌŚĶ¼![]() ÖŠ£¬Čō
ÖŠ£¬Čō![]() £¬
£¬![]() £¬ĻÖ½«Ķ¼
£¬ĻÖ½«Ķ¼![]() ÖŠµÄ
ÖŠµÄ![]() ČĘ×ŵć
ČĘ×ŵć![]() Ė³Ź±ÕėŠż×ŖČń½Ē
Ė³Ź±ÕėŠż×ŖČń½Ē![]() £¬µĆµ½Ķ¼
£¬µĆµ½Ķ¼![]() £¬ÄĒĆ“Ļ߶Ī
£¬ÄĒĆ“Ļ߶Ī![]() £¬
£¬![]() Ö®¼äÓŠŌõŃłµÄ¹ŲĻµ£¬Š“³ö½įĀŪ£¬²¢ĖµĆ÷ĄķÓÉ£»
Ö®¼äÓŠŌõŃłµÄ¹ŲĻµ£¬Š“³ö½įĀŪ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©ŌŚĶ¼![]() ÖŠ£¬Čō
ÖŠ£¬Čō![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬ĻÖ½«Ķ¼
£¬ĻÖ½«Ķ¼![]() ÖŠµÄ
ÖŠµÄ![]() ČĘ×ŵć
ČĘ×ŵć![]() Ė³Ź±ÕėŠż×ŖČń½Ē
Ė³Ź±ÕėŠż×ŖČń½Ē![]() £¬µĆµ½Ķ¼
£¬µĆµ½Ķ¼![]() £¬Į¬½Ó
£¬Į¬½Ó![]() ”¢
”¢![]() £®
£®
¢ŁĒóÖ¤£ŗ![]() £»
£»
¢Ś¼ĘĖć£ŗ![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com