
分析 (1)根据指数运算法则直接求出各数即可;
(2)利用(1)中所求得出尾数每4个一循环分别为:2,4,8,6,进一步计算得出210个位上的数字是4;
(3)利用(2)中的规律得出答案;
(4)利用(2)中规律得出3的指数变化与尾数的关系.
解答 解:(1)因为21=2,所以21个位上的数字是2;
因为22=4,所以22个位上的数字是4;
因为23=8,所以23个位上的数字是8;
因为24=16,所以24个位上的数字是6;
因为25=32,所以25个位上的数字是2;
因为26=64,所以26个位上的数字是4;
(2)由(1)可得出:尾数每4个一循环分别为:2,4,8,6尾数每4个一循环,
10÷4=2…2,
则210个位上的数字与第2个数据相等是4;
(3)∵2013÷4=503…1,
∴22013个位上的数字与第1个尾数相等是2;
(4)因为31=3,所以31个位上的数字是3;
因为32=9,所以32个位上的数字是9;
因为33=27,所以33个位上的数字是7;
因为34=81,所以34个位上的数字是1;
因为35=243,所以35个位上的数字是3;
…
∴尾数每4个一循环,
∵2014÷4=503…2,
∴32014个位上的数字是9.
故答案为:4;16,6;32,2;64,4;2;9.
点评 此题主要考查了数字尾数特征,根据指数的变化得出位置的变化规律是解题关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
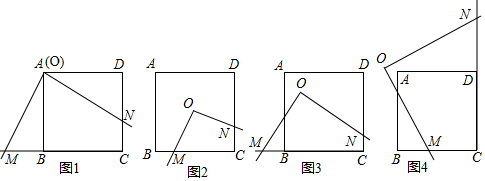
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 [问题提出]
[问题提出]查看答案和解析>>
科目:初中数学 来源: 题型:填空题
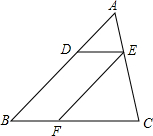 如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么S△CEF:S四边形DBFE=5:6.
如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么S△CEF:S四边形DBFE=5:6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
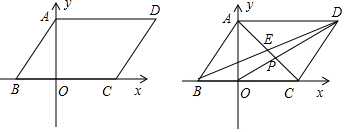
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减产值 | +10 | -12 | -4 | +8 | -1 | +6 | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
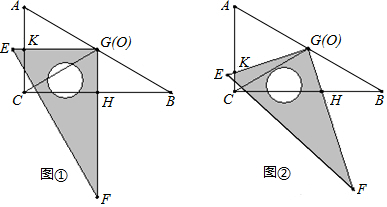
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com