
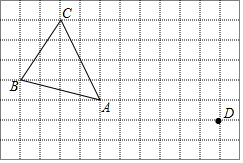
 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.分析 (1)根据三角形的面积公式即可得到结论;
(2)根据网格结构找出点B、C平移后的对应点E、F的位置,然后与点D顺次连接即可;
(3)根据网格结构和三角形的高线的定义作出图形即可;
(4)根据平移的性质,对应点的连线平行且相等.
解答  解:(1)S△ABC=4×4-$\frac{1}{2}×$1×4-$\frac{1}{2}$×2×3-$\frac{1}{2}$×2×4=7,
解:(1)S△ABC=4×4-$\frac{1}{2}×$1×4-$\frac{1}{2}$×2×3-$\frac{1}{2}$×2×4=7,
故答案为:7;
(2)如图所示;
(3)高线AD如图所示;
(4)AD与CF平行且相等.
故答案为:AD与CF平行且相等.
点评 本题考查了利用平移变换作图,平移的性质,熟练掌握网格结构,准确找出对应点的位置是解题的关键.


科目:初中数学 来源: 题型:解答题
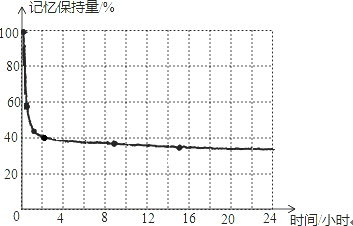 德国心理学家艾宾浩斯(H.Ebbinghaus)研究发现,遗忘在学习之后立即开始,而且遗忘的进程并不是均匀的.最初遗忘速度很快,以后逐渐缓慢.他认为“记忆保持量是时间的函数”,他用无意义音节(由若干音节字母组成、能够读出、但无内容意义即不是词的音节)作记忆材料,用节省法计算保持和遗忘的数量.他通过测试,得到了一些数据如下表,然后又根据这些数据绘出了一条曲线,即著名的艾宾浩斯记忆遗忘曲线,如下图.该曲线对人类记忆认知研究产生了重大影响.
德国心理学家艾宾浩斯(H.Ebbinghaus)研究发现,遗忘在学习之后立即开始,而且遗忘的进程并不是均匀的.最初遗忘速度很快,以后逐渐缓慢.他认为“记忆保持量是时间的函数”,他用无意义音节(由若干音节字母组成、能够读出、但无内容意义即不是词的音节)作记忆材料,用节省法计算保持和遗忘的数量.他通过测试,得到了一些数据如下表,然后又根据这些数据绘出了一条曲线,即著名的艾宾浩斯记忆遗忘曲线,如下图.该曲线对人类记忆认知研究产生了重大影响.| 时间间隔 | 记忆保持量 |
| 刚记完 | 100% |
| 20分钟后 | 58.2% |
| 1小时后 | 44.2% |
| 8~9小时后 | 35.8% |
| 1天后 | 33.7% |
| 2天后 | 27.8% |
| 6天后 | 25.4% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
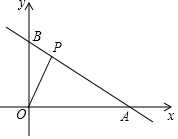 直线y=kx+6与x轴、y轴分别交于A、B两点,点A的坐标为(8,0).
直线y=kx+6与x轴、y轴分别交于A、B两点,点A的坐标为(8,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,∠ACB=90°,CD⊥AB,AC=5,BC=12,AB=13.点A到CD边的距离是$\frac{25}{13}$;点C到AB边的距离是$\frac{60}{13}$.
如图,∠ACB=90°,CD⊥AB,AC=5,BC=12,AB=13.点A到CD边的距离是$\frac{25}{13}$;点C到AB边的距离是$\frac{60}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
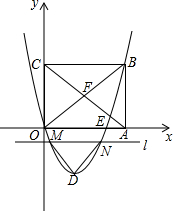 如图,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴上,点B坐标为(4,t)(t>0),二次函数y=x2+bx(b<0)的图象经过点B,顶点为点D.
如图,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴上,点B坐标为(4,t)(t>0),二次函数y=x2+bx(b<0)的图象经过点B,顶点为点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
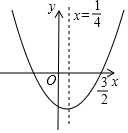 如图,已知二次函数y=ax2+bx+c的图象如图所示,则下列四个结论:①a+b+c<0;②a+c=b;③b=-2a;④4ac-b2<0,其中正确的结论有( )
如图,已知二次函数y=ax2+bx+c的图象如图所示,则下列四个结论:①a+b+c<0;②a+c=b;③b=-2a;④4ac-b2<0,其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com